ABSTRACT

The following explanation will be mostly related to the case of formations containing a negligible amount of conductive solids. A few additional remarks will be nevertheless brought forward regarding the case of shaly formations.

The symbols used in the present paper are:

R_xo = resistivity of a porous and permeable formation close to wall of hole.

R_w = resistivity of connate water

R_t = true resistivity of formation

R_m = resistivity of mud

R_mf = resistivity of mud filtrate

R_mc = resistivity of mud cake

R_{1 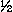in.inv} = value recorded with 1 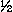- in. Microinverse device

R_{2 in. N} = value recorded with 2 - in. Micronormal device

h = thickness of mud cake

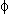= porosity

F = formation resistivity factor

The principle of the MicroLog and its application to the determination of the permeable beds traversed by a bore hole were given in an earlier paper¹.

RELATIONSHIP BETWEEN POROSITY AND R

It is known that, if a formation is practically clean, and is entirely impregnated with an electrolyte, the ratio of the

End_Page 81-------------------------

resistivity of the formation to the resistivity of the electrolyte is a constant, whatever the resistivity of this electrolyte. This constant designated as "Formation Resistivity Factor"² - or more simply "Formation Factor" - in turn is a function of the lithology of the formations, and mostly of the porosity. The following formula has been proposed to express the relationship between formation factor and porosity: F = [a]/[(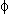)ⁿ] with F being the formation factor, 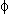the porosity, a and m two parameters depending on the nature of the formations.

Several values, variable mostly with the types of formations selected for the experiments, have been proposed for a and m, ^{2 3 4} but the curves showing F vs. 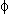for these various values of a and m are not much different from one another.

The evaluation of porosity through electrical measurements is based on the determination of the formation factor. For such a determination to be possible by measurements in situ it should be assumed that there exists one part of the porous formation under study which is saturated with a water of known resistivity, and that the resistivity of this part of the formation can be measured.

It occurs that, within a short distance from the wall of the hole, the connate water is entirely displaced by the penetration of mud filtrate and that the oil remaining in the pores, if any, is reduced to a small amount. The value generally accepted for the extension of htis flushed zone from the wall is about 2 - 3 in.; farhter on, the proportion of original fluids progressively increases until a distance is reached where the formation is completely uncontaminated.

End_Page 82-------------------------

When there is no residual oil in the flushed zone, as in the case of water-bearing formations, the formation factor - still supposing the formation is practically clean - will be equ equal to R_xo/ R_mf, with R_xo being the resistivity of the flushed zone, and R_mf the resistivity of the mud filtrate - and the porosity will be given by:

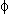[0.62(R_mf /R_xo)]^.15

In the case of oil-bearing formations, if ROS is the residual oil saturation, the formula will become:

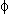[1]/[1 --ROS] 0.62 (R_mf/R_xo)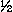^.15

The determination of the porosity thus depends on the knowledge of factors R_mf and R_xo.

The value of R_mf can be easily measured from a sample of mud or can be estimated from statistics (this equation will be further examined later on).

Factor ROS is not exactly known, but can be taken as approximately equal to the statistical value of the per cent per pore volume of residual oil in the cores, i.e., from about 10 to 30 per cent.

The value of R_xo cna be derived, within certain limits, from the MicroLog by means of appropriate interpretation charts as explained hereafter.

R_xo vs. MICROLOG READINGS

It is recalled that in the method of MicroLogging the measuring device essentially comprises a system of very small electrodes AM¹ M² at short distance from each other and borne by an insulating pad which is applied to the wall of the hole (Fig. 1). The measurements accordingly are related to very small volumes of material located behind the wall and shielded from the bypass

End_Page 83-------------------------

effect of the mud. Two curves are simultaneously recorded, with two distributions of electrodes corresponding to two depths of investigation: namely the 1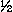 - in. Microinverse (AM¹ = 1 in. M¹ M² = 1 in. ) and the 2 - in. Micronormal (AM = 2 in. ).

In the case of a permeable and porous formation the pad is separated from the formation of the mud cake. The measurements are therefore affected both by the mud cake and by the formations behind and close to the wall, which, as said above, are flushed by the mud filtrate. The measurements are functions of R_xo, resistivity of the flushed zone, R_mc, resistivity of the mud cake, h, thickness of the mud cake, and d, diameter of the bore hole (the experience has shown that the resistivity R_m of the mud has only a secondary effect, which can be neglected for all practical purposes in most cases). The Micronormal curve is more affected by R_xo and less by the mud cake than the Microinverse.

The diameter of the bore hole is generally known from the bit size, or better from a section gage log, if such is available. The resistivity R_mc of the mud cake can be determined from a sample of mud, or from statistics. The measured values therefore depend only on two unknown factors, namely R_xo and h. Conversely the determination of R_xo and h is based on the two values measured with the Microinverse and Micronormal devices.

Because of the geometry of the various media involved in a MicroLog measurement, there is no possibility at the present time to determine mathematically the relationship between the factors involved: R_xo, h and the two MicroLog measurements. This relationship has therefore been established experimentally on laboratory models. The results of these determinations are given in the form curves, which constitute the basis of the interpretation charts.

End_Page 84-------------------------

Fig. 1. Schematic representation of Micrologging device in case of a porous and permeable formation.

Table 1.

End_Page 85-------------------------

Fig. 2. MicroLog interpretation charts.

End_Page 86-------------------------

DESCRIPTION OF INTERPRETATION CHARTS

A catalog of interpretation charts is now available for the user of electrical logging.(FOOTNOTE 5) Each chart of the catalog corresponds to a given value of R_mc at bottom-hole temperature. The range of values taken for R_mc extends by steps from 0.03 to 5. One sample chart is reproduced on Fig. 2.

Table 1 gives the values of R_mc and R_mf versus R_m and temperature. This table contains average values determined in the laboratory on numerous and varied samples of mud. These values are therefore only approximate, and the values of R_mc and R_mf should preferably be measured in each given case.

Each chart (Fig. 2) comprises from the left to the right:

1. A double set of curves, traced with R 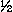in. inv. plotted in abscissas and R_xo in ordinates, both scales being logarithmic.* The solid curves correspond to constant values of R_{2in N}, and the dashed curves to constant values of mud cake thickness.
2. A grid containing several vertical scales corresponding to different hole diameters. This grid is actually divided into two parts: the left-hand part contains the scales for hole diameters equal to or larger than 8 in. up to 12 in., the right part of the scales for hole diameters equal to or smaller than 8 in. down. to 6 in. The value of R_xo is read on either of the 8 in. scales (heavy lines).
3. A grid giving the values of R_xo / R_mf corresponding to the values of R_xo, for different values of R_mf. The value of R_xo / R_mf is read on the right-hand scale (heavy line).

End_Page 87-------------------------

4. A grid giving the values of porosity corresponding to the value of R_xo/R_mf for different values of the per cent of residual oil in the flushed zone. The scale of porosity shown is derived from the application of formula F [0.62]/[(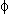)^2.15] .3
   *Note that the horizontal grid traced throughout the chart is not logarithmic but is made up of equally spaced lines. This grid is merely a guide for the graphic use of the charts.

DIRECTIONS FOR USE OF CHARTS

Directions for use of the charts (for the case of clean formations) are illustrated by means of an example, corresponding to the following values:

R_m at 160° = 0.35

R₁ 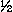in. inv. = 2 ohms-m

R₂ in. N = 2.5 ohms-m

Hole diameter: 10 in.

1. Enter the value of the temperature prevailing at the level of the bed under investigation, and the value of R_m corrected for this temperature into Table 1. The intersection of the column corresponding to the value of the temperature and of the line corresponding to the value of R_m gives the corresponding values of R_mc and R_mf, as derived from the average laboratory determinations.
   Example: With R_m at 150° = 0.35 and interpolating between the temperatures of 150° and 175°, the table gives R_mc = 0.8 and R_mf = 0.2.

End_Page 88-------------------------

If R_mc and R_mf are measured directly on a sample of mud, the values measured should be taken instead of the ones given by the table.
2. Choose the chart printed for the value of R_mc the closest to the value read on the table ( or measured on the sample).
   Example: The chart for R_mc=0.8 is used.
3. Start from the left-hand side of the chart. Plot the value of R_{1 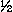in. inv.} read on the MicroLog, ( 2, in the example ) in abscissa. This gives point "a". Draw from "a" a vertical line up to the intersection in "b" with the curve (solid line) corresponding to the value of R_2in.N read on the MicroLog (2.5, in the example).
   The value of mud cake thickness is read on the dashed curves, by interpolation if necessary (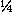 in., in the example).
4. Draw from "b" a horizontal line up to its intersection in "c" with the vertical scale corresponding to the value of the hole diameter (10 in., in the example). Draw from "c" a line along the trend of the oblique lines up to point "d" on the 8 in. scale (heavy line). The 8 in. scale is graduated and the location of point "d" gives the value of R_xo (3.7, in the example).
5. Draw from "d" a horizontal line until it crosses on point "e" the vertical scale corresponding to the value of R_mf - either read on the table, or measured (0.2 in the example). From "e" draw a line to the oblique direction shown on the grid until it crosses the right-hand scale (heavy line) on point "f".

End_Page 89-------------------------

The Values of R_xo / R_mf and R_mf / R_xo are read on the corresponding scales at the level of point "f": respectively 17 and 0.058 in the example.
6. Draw from " f " a horizontal line until it crosses the vertical scale corresponding to the value of residual oil saturation, which is supppsed equal to 15 per cant in the present example (point "g". From "g" draw a line parallel to the oblique direction show on the grid until it reaches the right-hand scale (heavy line) on point "h".
7. Read the value of porosity at the level of "h": 25 per cent in this example. The corresponding value of the formation factor is given on the next scale, in this example 13.

SECOND EXAMPLE (CLEAN FORMATIONS)

R_mc measured = 0.8

R_mf measured = 0.16

Hole diameter = 6 in.

R_{1 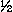in.inv}=5.5

R_{2 in. N}= 6

See line a'b'c'd'e'f'g'h'i' on the chart.

Results: If the residual oil saturation is assumed to be equal to 10 per cent:

Porosity: 15 per cent

Formation factor: 36

ACCURACY OF THE DETERMINATION

Determination of porosity from the MicroLog curves comprises two steps:

1. Translation of the MicroLog readings into values of R_xo / R_mf.
2. Translation of the values of R_xo / R_mf int values of porosity.

End_Page 90-------------------------

Degree of accuracy obtained in the two successive operations will now be discussed:

1. The curves printed in the catalog were determined by means of laboratory models and of electrical circuits such that the field conditions be reproduced as closely as possible. Some differences may, however, still exist between the laboratory and the field conditions in certain cases. In particular, it may sometimes happen that the field pad does not fit exactly the diameter of the hole, which may influence the measurements to a certain extent.
   It is furthemore seen on the charts that there is a region (the lower part) where the slope of the curves is very great, and even close to the vertical. If a point is plotted in this region the usual errors in the measurements of R_{1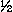 in.inv.} and R_{2 in.}^N will lead to a much greater error on the corresponding value of R_xo. This zone corresponds to comparatively high values of R_xo. Accordingly, since R_xo is greater as porosity is smaller, a good accuracy in the determination of R should be expected in formations whose porosity is not too low.
   The charts also show that, for a given value of R_xo, the thicker the mud cake, the greater the slope of the curve, but that the accuracy is not too much impaired by thick mud cakes when R_xo is not too great.
   To define these effects, it can be said that, according to the experience available to date, good results are obtained when the porosity of the formations is higher than 20 per cent, provided the thickness of the mud cake does not exceed about i in. Fair determinations are still possible for lower values of porosity, down to 15 per cent and even less, if the mud cake Thickness does not go beyond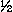 in.

End_Page 91-------------------------

It is also recalled that the value found for R_xo depends on the chart chosen for the interpretations, i.e., on the value taken for R_mc. The accuracy in the value arrived at for R_xo R_mf is thus finally affected by the accuracy in the determination of R_mc and R_mf. As already said, the values given in Table 1 are averages, and the exact values of and R_mc in a given case may depart from the respective averages appreciably. It is therfore advisable to measure R_mc and R_mf directly on samples taken in each case.
2. The value of the porosity of a formation is related to the value of the formation factor through empirical formulas which are also averages of numerous determinations, and here again the true relationship in each case may be somewhat different from the average one. In addition to this, the presence of residual oil in the flushed zone is also a cause of uncertainty. Finally, the above considerations are related only to the case of substantially clean formations. In the case where the formations contain an important amount of conductive solids, additional corrections are necessary, as explained hereafter.

CASE OF SHALLY SANDS

In the case of shaly formations, the conductive solids add their conductivity to that of the network of electrolytes in the pores. If (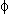)e is the effective porosity of the formation, the value of R_xo is lower then it would be in the clean formation with the same porosity (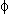)e. Accordingly, the porosity value derived with the charts from the MicroLog readings opposite a shaly sand is only an "apparent value," which is greater than the effective porosity of the formations.

End_Page 92-------------------------

The determination of the correction to be introduced into the value derived from the Microlog to obtain the exact value of the effective porosity is a difficult problem, now still under study.

Pending further experimental and theoretical developments, it seems nevertheless possible to propose a provisory equation, based on purely mathematical conceptions, and applicable to the case where the conductive solids are disseminated in the pores:

i.e. (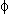)e = (a X R_mf / R_xo)^1/m -- (a X R_mf / R_cs)^1/m

where R is the resistivity of the formation due to the conductive solid network only, i.e., the resistivity the formation would have if everything but the conductive solid were of very high resistivity.

The first term of the above formula is equal to the apparent porosity, i.e., to the value given by the charts. The second term represents the value of the correction for colloids. Table 2 gives numerical values for this correction, computed with a and m being taken respectively to 0.62 and 2.15, as for the curves.

As already said, the above formula is purely theoretical and needs experimental checks. Furthermore, in the case of the presence of laminating shales, the corresponding formula would certainly be more complex, and the correction values somewhat different. Table 2 should therefore be considered as giving only orders of magnitude.

It is anyway interesting to notice that the correction is proportional to R_mf. In other words, the more conductive the mud, the smaller the relative effect of the conductivity of the shales on the value of R_xo. The use of salty mud is therefore advisable to improve the accuracy of porosity determinations in shaly sands.

End_Page 93-------------------------

The salinity of the mud should not, however, be too great in order not to affect the curves adversely, in particular the SP curve. It seems that a value of mud resistivity equal to about five times the resistivity of the connate waters would be a good compromise.

The following examples are relative to formations which may be considered negligible amounts of conductive solids. Besides, in these examples porosity values were computed without taking the possible presence of residual oil into account.

Fig. 3 shows the conventional curve and the MicroLog recorded through the Yegua formations in a Gulf Coast well (Well No. 1).

The data for this well are the following:

Bit Size : 9 7/8 in.

R_m = 1.2 ohm-m at BHT(150°F.).

Table 1 gives the corresponding values for R_mc and R_mf equal respectively to 1.14 and 0.99. the chart for R_mc=1.2 was therefore chosen for the interpretation.

The values for porosity computed from the logs for the three sand intervals, I, II, III, shown on the figure, are tabulated hereafter. The average values for each of the above sections are matched with the average values derived from core analysis, which are given in the right-hand column.

In this analysis the intervals, a, b, c, d, have been excluded since they contain a substantial amount of shale according to the MicroLog, the SP curve and the conventional resistivity curves.

An accompanying table gives further examples of comparative average porosity values determined from the MicroLog and from core analysis in various wells and for various formations of the Gulf Coast.

End_Page 94-------------------------

Fig. 3. Example of quantitative interpretation of MicroLog (clean formations of high porosity).

Table 2. TABLE OF TENTATIVE CORRECTIONS TO BE SUBTRACTED FROM THE POROSITIES OBTAINED (PER CENT), ACCORDING TO THE VALUE OF R_mf AND R_cs

End_Page 95-------------------------

Figure 4 shows a section of a well drilled through the shales and consolidated sands in North Texas. The data for the well are the following:

Bit size: 7 7/8 in.

R_m=0.6 ohm-m at 123°F.

Table 1 gives R_mc = 1.09 and R_mf = 0.69. The chart for R_mc = 1 is chosen. The porosity values derived from the MicroLog in intervals I and II, where core analyses are available, are tabulated hereafter:

In the averages of well No. 8 the values found in sections a (4,991 ft.) and b (5,023 ft.), which correspond to comparatively tight beds, have been discarded.

In addition to this, the following examples from Mid-Continent are given hereafter: Mid-Continent Wells -- MicroLog vs. Core Porosity

CASE OF VERY SHALLOW INVASION

In formations with high porosity and permeability the invasion often happens to be so shallow that the MicroLog readings

Table. OTHER EXAMPLES -- MICROLOG VS. COR POSOSITY

Table. Mid-Continent Wells -- MicroLog vs. Core Porosity

End_Page 96-------------------------

Fig. 4. Example of quantitative interpretation of MicroLog (clean formations of medium porosity).

Table. WELL NO. 1--GULF COAST--YEGUA

End_Page 97-------------------------

can be somewhat affected by the uncontaminated formations beyond the invaded zone.

Two cases should be considered:

(a) Waterbearing Formations In most cases the connate water has a resistivity less than the resistivity of mud filtrate, so that the resistivity R_t of the uncontaminated formation is less than R_xo. If the invasion is so shallow that the measurements made with the MicroLog involve a part of the noninvaded zone, the recorded values are reduced with respect to the values which would be obtained in the case of a deep invasion, all other factors remaining the same. Furthermore, the decrease is more important with Micronormal than with the Microinverse. The measurements therefore, when plotted on the charts, lead to an apparent value for R_xo which is lower than the true value, and the porosity determined from the MicroLog is greater than the true porosity.

The presence of a shallow invasion very often can be ascertained from the characteristics of the logs: the readings with the conventional devices are all very low, and the separation between the short normal and the long normal curve is much reduced, and is even nil. Accordingly, when such features are observed on the conventional logs, the interpretation of the MicroLog should be made with great caution, especially from the quantitative standpoint.

It should be furthermore said that, in many cases, the separation between the two MicroLog curves is reduced to nil, and is even negative. This of course is a very clear indication, and the corresponding formations are easily eliminated from the quantitive analysis.

It may be recalled also that in high permeability

End_Page 98-------------------------

sands there is an appreciable part of the mud cake which builds up inside the pore space of the formations. This part of the mud cake has a resistivity higher than that of the mud cake formed outside, to a ratio which is equal to the formation factor of the formation, i.e., at least 5. As a result, the values measured with the Microinverse are increased more than those measured with the Micronormal. This effect therefore contributes to create a negative separartion on the MicroLog.

Fig. 5 shows, as an example, two portions of the logs recorded through water-bearing formations of high porosity in the Gulf Coast. Section 1 shows a large separation the readings of the short and the long normal, which corresponds to a rather deep invasion; the porosity derived from the MicroLog is equal to 30 percent, against 32 per cent given by core analysis. Opposite Sections 2, 3, 4, and 5 the two normal curves are very low and close to each other, which indicates a shallow invasion.

The separation between the two MicroLog curves accordingly is smaller than on Section 1, and the porosity derived from the MicroLog would be much higher than the true porosity. Opposite Sections 6 and 7 the two normal curves practically coincide, and the separation on the MicroLog curves is negative. Bed 8 gives a positive separation on the MicroLog, whereas the two normal curves coincide. It is likely that some invasion took place in this case, but the bed is so thin that the presence of this invasion cannot be reflected on the short normal curve.

(b) Oil-bearing formations: The true resistivity R_t of an oil-bearing formation may be greater or smaller than R_xo depending on the ratio R_w to R_{m 2/3}, on the water saturation.. etc. ... For low water saturation, however, and when the mud

End_Page 99-------------------------

Fig. 5. MicroLog in the case of shallow invasion; water-bearing sands of high porosity.

Table. WELL NO. 8--NORTH TEXAS

End_Page 100------------------------

is not abnormally fresh, R_t is usually higher than R_xo, which amounts to an increase of the values recorded with the MicroLog and of the separation between the curves. The values of porosity from the MicroLog are therefore too low.

It is again possible in some cases to ascertain, from the comparisons of the MicroLog and other curves, whether the invasion is shallow enough for the MicroLog readings to be affected by R The comparison, however, is not so easy and accurate as in the case of water-bearing formations.

MCROLOGGING A HELP IN SATURATION DETERMINATION

It is known that the evaluation of the fluid saturation in a porous bed from the electrical curves can be made by means of Archie's formula:

S = ([F X R_w]/[R_t])^1/m

where

S = water saturation in per cent of pore space

F = formation resistivity factor

R_w = resistivity of connate water

R_t = true resistivity of formation

For the application of the formula, the value of a formation factor, which was formerly determined on cores in the laboratory, can now be obtained by means of a MicroLog. As seen in this article, the interpretation charts contain a scale which gives the values of the formation factor (opposite the values of porosities) as derived from the values read on the MicroLog.

A complete discussion about the determination of the two other factors, R_w and R_t, would be beyond the scope of the presentarticle. The following brief indications regarding them will be recalled:

The resistivity R_w of the connate water is connected with amplitude of the deflection of the SP curve observed opposite

End_Page 101------------------------

the bed. When the bed is thick enough the amplitude of the deflection is equal to the "Static SP," i.e., to the total e.m.f. which generate the spontaneous current -- which in turn can be approximately taken as being equal to - K log R_m / R_w (R_m mud resistivity). In this expression, K is a coefficient which has been found empirically equal to about 90 in many cases, but which may vary between about 50 and 120, depending on the conditions found in the regions under survey.

It should be recalled that the expression of the Static SP is actually more complex, and that, accordingly, the expression -- K log R_m / R_w Should be considered as giving only a convenient way to a fast estimation of the order of magnitude of R_w. Needless to say that the value of R_w should be preferably measured on samples of connate water, whenever such samples are available.

The value of the true resistivity of the bed is obtained, in most cases, from the conventional resistivity curves, provided the thickness of the bed is great enough, or form such new devices as the Laterologand/or the induction log - with the help of appropriate departure curves, if necessary.

This procedure will be illustrated with the following example: Fig. 6 shows the MicroLog and the conventional curves recorded in a North Texas well. Several porous and permeable sections are indicated by the MicroLog (crosshatched areas on the figure). Among them Section A will be considered in detail.

If the thin tight streak denoted as "a" is discarded, the quantitative analysis of the MicroLog in Section A shows that the formation factor and the porosity vary within comparatively narrow limits throughout the section. In other words, the whole

End_Page 102------------------------

Fig. 6. Data for well No. 15, North Texas area; bit size = 7 7/8 in.; R_m (at BHT) = 0.7 ohm/m.

End_Page 103------------------------

section be taken as being one single fairly homogeneous bed. The total thickness of this bed is about 70 ft., so that the effect of the adjacent formations on the values recorded on the conventional curves, even on the long lateral curve, can be replaced.

1. The average value of R_xo / R_t throughout the section, as derived from the MicroLog charts, is equal to 40, and the average formation factor, supposing 15 per cent residual oil in the flushed zone, is about equal to 30. (The corresponding value of the average porosity would be about 17 per cent.)
2. The ampitude of the deflection of the SP curve is equal to -- 120 mv. According to the experience gathered in the region where the well is located, the value of the K coefficient would be around 90, the corresponding value or R_m / R_w is, therefore, about 20. Since R_m is equal to .7 at BHT, R_w can be taken equal to 0.035, as a first approximation.
3. Value of R_t -- The average apparent resistivity read on the long lateral throughout the section is equal to 220 ohms./m which, after correction with the departure curves for beds of infinite thickness, gives gives an average value of 150 ohms'm for R_t.

Taking the exponent of Archie's formula equal to 2, the water saturation in the uncontaminated zone, therefore, is equal to

[EQUATION]

or around 10 percent.

The computation of water saturation in the other permeable and porous sections is not so easy, because these sections are

End_Page 104------------------------

comparatively thin, and their true resistivities cannot be determined accurately from the conventional logs. Considering, for example, Section B, whose thickness is about 4 ft. according to the MicroLog, it appears, that the long lateral curve is very much distorted and cannot be relied upon; the long normal curve, nevertheless, is easily readable. Because of the presence of the tight formations above and below the bed, it is likely that the value read on the 1 on normal, namely 100 ohms, is an upper limit for R_t. A reasonable lower limit can be taken equal to 50 ohms. Furthermore, the SP curve is not entirely developed, but it can be assumed that the value of R w is the same as in Section A, i.e., 0.035 ohm/m. The MicroLog gives, for the formation factor, a value about equal to 35 -- hence the water saturation would be comprised between [EQUATION], or 11 per cent, and [EQUATION], or 15 percent. Values of saturation of the same order would be found for the other thin sections.

Almost all the permeable sections were gun perforated: the well produced 214 bb1. of oil per day through a 16/64-in. choke.