About This Item
- Full TextFull Text(subscription required)
- Pay-Per-View PurchasePay-Per-View
Purchase Options Explain
Share This Item
The AAPG/Datapages Combined Publications Database
Oklahoma City Geological Society
Abstract
Component Dip Nomogram
ABSTRACT
The determination of the  magnitude
magnitude and direction of component dip from the
and direction of component dip from the  magnitude
magnitude and direction of the true dip by means of a circular nomogram.
and direction of the true dip by means of a circular nomogram.
When the  magnitude
magnitude and direction of a true dip of a plane are given the
and direction of a true dip of a plane are given the  magnitude
magnitude of the component dip in a vertical plane in any direction may be very conveniently solved for routine work by means of a circular nomogram.
of the component dip in a vertical plane in any direction may be very conveniently solved for routine work by means of a circular nomogram.
Let (![]() ) be the true dip and (
) be the true dip and (![]()
![]() ) the component of the true dip in a direction which makes an angle (o) with the direction of the true dip; then it is well known that:
) the component of the true dip in a direction which makes an angle (o) with the direction of the true dip; then it is well known that:
![]() (1)
(1)
or,
![]() (2)
(2)
or, if (m) is a scale factor the constructional determinant for the nomogram may be written:
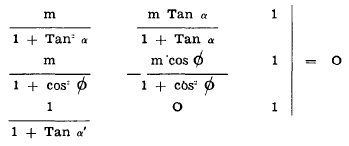 (3)
(3)
Let:
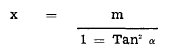 (4)
(4)
and
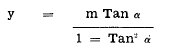 (5)
(5)
then, eliminating (Tan ![]() ) between these two equations, it is found that:
) between these two equations, it is found that:
![]() (6)
(6)
which is the equation to a circle passing through the origin whose radius is equal to (m). Thus, the scale for the true dip (![]() ) is therefore the upper half of the circumference of a circle of radius (m); similarly, the scale for the direction (O) is the lower half of the circumference of the same circle, and the scale for the component dip (
) is therefore the upper half of the circumference of a circle of radius (m); similarly, the scale for the direction (O) is the lower half of the circumference of the same circle, and the scale for the component dip (![]()
![]() ) is the diameter of this circle separating the (
) is the diameter of this circle separating the (![]() ) and (O) scales.
) and (O) scales.
The completed nomogram is shown in , together with an example from which it is seen that by a straight line alignment of the scales that when (O) = 36 degrees and (![]() ) = 30 degrees, the component dip (
) = 30 degrees, the component dip (![]()
![]() ) = 25 degrees.
) = 25 degrees.
COMPONENT DIP NOMOGRAM
End_of_Record - Last_Page 188-------
Pay-Per-View Purchase Options
The article is available through a document delivery service. Explain these Purchase Options.
| Watermarked PDF Document: $14 | |
| Open PDF Document: $24 |
