The AAPG/Datapages Combined Publications Database
AAPG Bulletin
Full Text
![]() Click to view page images in PDF format.
Click to view page images in PDF format.
AAPG Bulletin, V.
DOI: 10.1306/08171514211
Restorations of faulted domes
Mohammed M. Al-Fahmi,1 Andreas Plesch,2 John H. Shaw,3 and John C. Cole4
1Department of Earth Sciences, University of Oxford, South Parks Road, Oxford OX1 3AN, United Kingdom; [email protected]
2Department of Earth and Planetary Sciences, Harvard University, 20 Oxford Street, Cambridge, Massachusetts 02138; [email protected]
3Department of Earth and Planetary Sciences, Harvard University, 20 Oxford Street, Cambridge, Massachusetts 02138; [email protected]
4Sasol Canada, Suite 1600, 215-9th Avenue SW, Calgary, Alberta, Canada T2P1K3; [email protected]
ABSTRACT
We illustrate recently developed techniques of three-dimensional (3-D) geomechanical structural restoration applied to resolve the kinematics of deformation in the sedimentary cover above mobile salt. Our study area is one of the hydrocarbon-bearing domes in eastern Arabia. We used 3-D seismic reflection and well data to build a 3-D structural geomodel for the well-imaged part of the sedimentary cover. The geomodel includes faults and a 3.2-km (2-mi) thick section of Permian to Cenozoic sediments and is restored from the Jurassic to the present day. The development of the structures is characterized by stages of normal faulting in the Jurassic and Cretaceous and a subsequent stage of low-amplitude folding in the Late Cretaceous. We interpret that the development of the structures in the sediment cover is caused by the movement of a deep, nonpiercing salt pillow. The structures grew under the control of gradually changing deforming mechanisms, from dominantly faulting to folding. The transition from normal faulting to domal folding is indicative of a reactive salt diapir. These restoration results improve our understanding about the kinematic history of the structures developed within the Jurassic and Cretaceous sedimentary section, which contains most of the hydrocarbon resources in Arabia. Moreover, they illustrate the potential of geomechanical restoration methods to investigate structures above mobile salt systems.
INTRODUCTION
Characterization of subsurface structures requires the integration of data and interpretations in a three-dimensional (3-D) modeling framework, with consideration of how the structure developed over geologic time. Such a geomodeling approach improves knowledge on where, when, and how structures developed and subsequently guides the tectonic interpretation. The validity of geomodels is commonly subject to interpreter judgments (e.g., Bond et al., 2007) but can be verified and enhanced by certain objective methods including structural restoration. Structural restoration techniques have been used for decades to validate seismic interpretations and derive a general framework for stratal geometries (e.g., Chamberlin, 1910; Dahlstrom, 1969; Gibbs, 1983; Erslev, 1991; Gratier and Guillier, 1993; Shaw et al., 1994; Williams et al., 1997; Allmendinger, 1998; Rouby et al., 2000; Griffiths et al., 2002; Maerten and Maerten, 2006; Moretti et al., 2006). Various restoration techniques have proven valuable in areas with large uncertainties in geomodeling, which may result from limited data and/or from spatially complex structures. Furthermore, the techniques are regularly applied to reduce the uncertainties in the modeling of the subsurface structures targeted for exploration and development of hydrocarbon resources.
Traditional restoration techniques, however, retain the major limitations of Dahlstrom’s model, which applies geometric and kinematic rules in two-dimensional domains. Dahlstrom (1969) assumed plane strain to describe structures and rationalized that valid geologic cross sections must preserve cross-sectional areas and line lengths of folded strata through restoration. The assumption of conservation of bed line lengths presumed the accommodation of off-fault strain by bed-parallel, flexural slip. The current techniques that use Dahlstrom’s assumptions have widespread application in contractional and extensional geologic settings, but their application is limited for inherently 3-D structures, including those that involve salt (e.g., Rowan and Ratliff, 2012).
In this study, we seek to overcome the limitations of traditional restoration methods through the application of a new 3-D geomechanical restoration technique (e.g., de Santi et al., 2003; Mueller et al., 2005; Muron et al., 2005; Guzofski et al., 2009; Durand-Riard et al., 2010) to a structure that is driven by mobile salt. This method has proven effective at sequentially restoring contractional, extensional, and strike-slip structures (e.g., Maerten and Maerten, 2006; Moretti et al., 2006; Plesch et al., 2007; Durand-Riard et al., 2013; Li et al., 2013). However, restoration of salt-related structures is difficult because of the inherent limits of the simple constitutive laws and continuum (finite-element) based methods implemented in these restoration tools. Thus, our approach to the problems of salt-related structures is to focus on deciphering components of folding and faulting within strata above the salt. We make no assumption about salt geometry, budget, and halokinesis. We test this approach on a faulted salt dome, where faults grew and branched to cut through roof strata, producing complex geologic structures that trap hydrocarbon resources. Our goal is to assess if the restoration techniques can recover viable deformation kinematics, resolve the relative contributions of folding and faulting in the growth of the structure, and infer indirectly the history of salt motion.
GEOLOGIC BACKGROUND
The study area is an onshore, multi-reservoir hydrocarbon field, located on the western periphery of the north basin of the Persian Gulf (Figure 1). The anticlinal structure is one of many domes in the region attributed to the deeply buried salt diapirism beneath the eastern Phanerozoic sequence of the Arabian plate (e.g., Powers et al., 1966; Edgell, 1991). Buried salt domes are interpreted on the basis of the geometry of the cover sediments aligned with strong negative gravity anomalies (e.g., Edgell, 1991). The salt is interpreted to be part of the infra-Cambrian Hormuz salt, which is exposed within the Zagros and Makran mountain belts of Iran (e.g., Talbot, 1998).
 Figure 1. (A) Regional map of the Persian Gulf region and the Hormuz salt distributions, modified after Bahroudi and Koyi (2003). The location of the study area is highlighted in the dashed square. (B) Index map highlights location of the Gulf region and the geologic traverse in Figure 1C. (C) Geologic traverse (XX′) shows the sedimentary successions above Hormuz salt, modified from Konert et al. (2001), courtesy of GeoArabia, and after Alsharhan and Nairn (1997).
Figure 1. (A) Regional map of the Persian Gulf region and the Hormuz salt distributions, modified after Bahroudi and Koyi (2003). The location of the study area is highlighted in the dashed square. (B) Index map highlights location of the Gulf region and the geologic traverse in Figure 1C. (C) Geologic traverse (XX′) shows the sedimentary successions above Hormuz salt, modified from Konert et al. (2001), courtesy of GeoArabia, and after Alsharhan and Nairn (1997).
Approximately 160 Hormuz salt diapirs have extruded in the Zagros Mountains and its foreland, and some islands and peninsulas in the Gulf owe their existence partly to movement of the Hormuz salt (e.g., Kent, 1958, 1979; Talbot and Jarvis, 1984). The extent of the salt in the Zagros and the Gulf region is deduced from emergent diapirs. Throughout this region, the depositional salt thickness is large enough to develop salt ridges, pillows, and diapirs (e.g., Callot et al., 2007).
The stratigraphic section above the salt consists of the alternating carbonates and clastics sections of the Arabian sedimentary basin, which developed during the last 650 m.y. (Figure 1C). The basin sediments unconformably overlie the Arabian shield and dip very gently and uniformly toward the Gulf (e.g., Powers et al., 1966). The basin sediments thicken from about 4 km (2.5 mi), at the western margin of the basin near the Arabian shield, to about 10 km (6.2 mi) in the Gulf region (e.g., Al-Amri, 2013; Sharland et al., 2013). The lithological variations of the basin sequences are controlled by the interaction of eustasy and sediment supply, with regional and local tectonic influences (e.g., Ziegler, 2001). In addition to salt movement, the sediments in the basin are influenced by reactivation of the fault systems within the Precambrian basement during a mid-Carboniferous deformational event known as the Hercynian orogeny (e.g., Konert et al., 2001). Subsequent reactivation of the Precambrian faults during the Cretaceous and Neogene produced additional growth of the anticlinal structures in eastern Arabia (e.g., Faqira et al., 2009).
The tectonic events that influenced the eastern margin of the Arabian plate include the Late Cretaceous obduction of the Semail ophiolitic nappe and the Arabian–Eurasian collision (e.g., Searle and Cox, 1999; Mouthereau et al., 2012). These contractional tectonic elements are not, however, manifesting directly in the study area. The study area is within the passive region of the western and north region of the Gulf. Most of the deformation (shortening) of the Arabian–Eurasian collision was accommodated to the east within the Zagros simply folded belt and underthrust Arabian margin (e.g., McQuarrie and Van Hinsbergen, 2013).
METHODS
Three-Dimensional Geomodeling
We developed a 3-D geomodel to define the subsurface structure in the study area on the basis of log interpretations of 48 vertical wells and 3-D seismic reflection data acquired in 2006 (Figure 2). The quality of the well log information varies across the field area because of well locations, available log types, and the logged intervals. Nevertheless, these well logs provide relatively dense information for most areas of the dome, with the most precise constraints on the Jurassic section, which host the main target zones for hydrocarbon production. The geomodeling of peripheral areas of the dome and strata older than Jurassic is based on the interpretation of a few well logs that are tied to the 3-D seismic reflection data. The seismic data were processed (prestack time migration with post-stack enhancement) and depth-migrated utilizing check shot velocity data. Seismic imaging for the rock strata beneath the Permian formations is poor. Therefore, the geomodel does not include structures from the poorly imaged part of the roof strata or the deeply buried salt.
 Figure 2. Combined view of a section and time slice from the three-dimensional seismic reflection data used in our study. This perspective highlights some of the structural elements incorporated in our model, including the domal shape of the fold and associated normal faults. The image of the seismic reflection below Permian (at the center of the seismic layer) is poor and limits our ability to directly resolve the geometry of the salt body.
Figure 2. Combined view of a section and time slice from the three-dimensional seismic reflection data used in our study. This perspective highlights some of the structural elements incorporated in our model, including the domal shape of the fold and associated normal faults. The image of the seismic reflection below Permian (at the center of the seismic layer) is poor and limits our ability to directly resolve the geometry of the salt body.
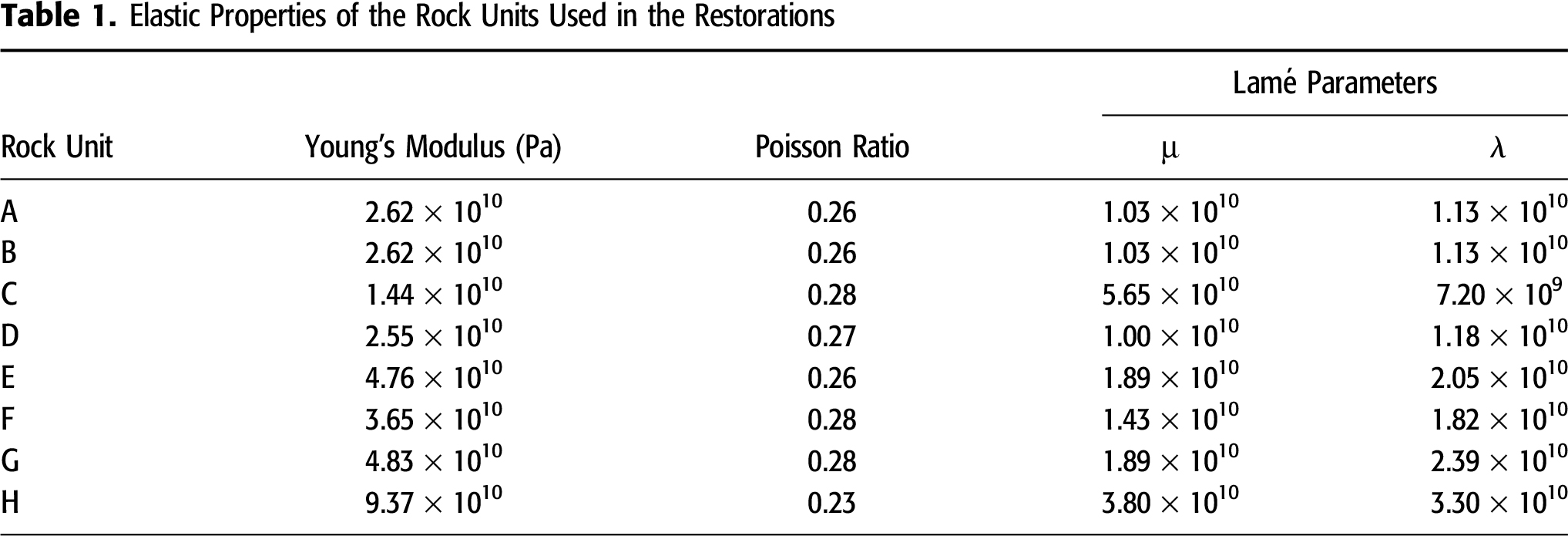
Instead, the study focuses on the relatively well-imaged section of the sedimentary rocks formed from Permian to Cenozoic (Figure 1C). The 3-D geomodel includes surfaces that correspond to major stratigraphic layers and the resolvable faults interpreted from seismic reflection data (Figure 3). The division of the sedimentary section into eight units was based on the analysis of an existing one-dimensional geomechanical model built from two wells (Table 1). The properties for each unit were defined by depth-weighted averages of density and elasticity moduli.
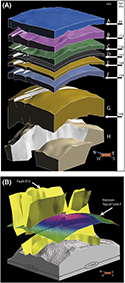 Figure 3. The structural elements in the geomodel. (A) Expanded view of the three-dimensional geomodel with the eight mechanical units with the corresponding geologic ages at the unit contacts and (B) the same geomodel but the units are removed except the bottom unit to show fault geometry and the top layer of unit F. Vertical exaggeration is 3:1. The model area is about 11 km (6.8 mi) along an east–west cross section and 9.6 km (6 mi) along a north–south cross section.
Figure 3. The structural elements in the geomodel. (A) Expanded view of the three-dimensional geomodel with the eight mechanical units with the corresponding geologic ages at the unit contacts and (B) the same geomodel but the units are removed except the bottom unit to show fault geometry and the top layer of unit F. Vertical exaggeration is 3:1. The model area is about 11 km (6.8 mi) along an east–west cross section and 9.6 km (6 mi) along a north–south cross section.
Three-Dimensional Structural Restoration Techniques
We employed a 3-D geomechanical restoration method that is based on continuum elastic modeling implemented as a structural restoration plugin (e.g., Muron et al., 2005; Guzofski et al., 2009; Durand-Riard et al., 2010, 2013) within Gocad (Mallet, 1992). The governing constitutive law is linear elasticity, with mechanical properties that can vary spatially. The method also ensures fault compliance during restoration. Accordingly, stress, strain, and displacement fields are path independent. Fundamentally, if the shape of an elastic material changed under load, it can return to the initial shape (or volume) if the same load is inverted. The load is treated as cumulative, accepting the principle of superposition, which states that two stress fields may be superimposed to yield the results for combined loads. The superposition principle is extended to strain and displacement fields in the linear elastic models. Thus, our restorations can be regarded as retrodeformation for the folds and faults included in the 3-D geomodel (Figure 3).
The elastic constitutive law implemented in the restoration is a simple approximation of more complex deformation behaviors in natural structures. In an attempt to address these limitations, we restore the structure in small increments of deformation with displacement boundary conditions governed by sequential restoration of growth strata. Avoiding clear pitfalls (Lovely et al., 2012), such approximations have been shown to yield kinematically valid restorations with reasonable strain signatures (e.g., Muron et al., 2005; Maerten and Maerten, 2006; Guzofski et al., 2009; Durand-Riard et al., 2010, 2013).
To facilitate the restoration, we generated a tetrahedral mesh of the geomodel and restored the structure using a finite-element approach based on volume conservation and global strain minimization criteria (Lepage, 2003). Each mechanical unit in the model was assigned values for density and Lamé’s elastic constants as shown in Table 1. The restorations were driven by implementing a displacement boundary condition to the top of the model corresponding to the flattening of a stratigraphic layer (Figure 4). Each unit was restored to a flat datum using one pin point as a boundary condition. The method allows for a more extensive set of boundary conditions such as side-wall displacements, pin lines, and pin walls. However, we limited boundary conditions of our model to the displacement of the target restoration layer because this most directly reflected the vertical tectonic forcing related to the underlying salt dome. Moreover, we used only a simple pin point for reference to allow for fully 3-D displacement fields that are expected for salt-related structures. The restoration displacement vectors for the model were calculated using the finite-element method (e.g., Muron et al., 2005; Zienkiewicz et al., 2005; Maerten and Maerten, 2006; Moretti et al., 2006), combined with a dynamic relaxation algorithm (e.g., Papadrakakis, 1981) that ensures fault compliance and thus enables restoration of complex fault systems (e.g., Muron et al., 2005; Durand-Riard et al., 2013). We performed sequential restorations of our geomodel and analyzed these displacement fields to resolve the folding and faulting kinematics in the corresponding sedimentary cover.
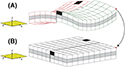 Figure 4. Two-step model to explain the concept of structural restoration. The restoration method calculates a displacement field that translates the elements of (A) a deformed sedimentary layer to (B) an undeformed shape that represents the original geometry of the sedimentary layer.
Figure 4. Two-step model to explain the concept of structural restoration. The restoration method calculates a displacement field that translates the elements of (A) a deformed sedimentary layer to (B) an undeformed shape that represents the original geometry of the sedimentary layer.
The growth of the dome was analyzed from the geometry of the top surfaces derived from the sequential restorations (Figure 5A). The derived top surfaces are presented as cross-sectional profiles to demonstrate the difference in elevations between the center and distal ends of the dome. The dome profiles present both geometry and relative age, which is estimated from the age of the units that were used as restoration datums. Similarly, the evolution of the faults is described using the evolution of fault displacements. The fault displacement was computed from the distance between the initial and final position of the points (i.e., nodes of finite elements) on both sides of the fault after each restoration step.
 Figure 5. Evolution of the dome structure from the top of unit F. (A) View for the locations of cross sections (B) S1, (C) S2, and (D) S3. Profiles display dome geometry at relative geologic times as follows: 6 = present time, 5 = 89 Ma, 4 = 112 Ma, 3 = 136 Ma, 2 = 141 Ma, and 1 = 154 Ma. F1, F2, and F3 are labels for faults 1, 2, and 3, respectively (see Figure 6).
Figure 5. Evolution of the dome structure from the top of unit F. (A) View for the locations of cross sections (B) S1, (C) S2, and (D) S3. Profiles display dome geometry at relative geologic times as follows: 6 = present time, 5 = 89 Ma, 4 = 112 Ma, 3 = 136 Ma, 2 = 141 Ma, and 1 = 154 Ma. F1, F2, and F3 are labels for faults 1, 2, and 3, respectively (see Figure 6).
RESULTS AND ANALYSIS
Doming of the Sedimentary Cover
The dome evolution from the restoration results of unit F is presented in Figure 5. The current dome structure of unit F is presented in red profiles, which marks the last stage (labeled no. 6) of the dome development. The profiles in Figure 5 are colored and labeled in a systematic manner, so stages 5, 4, 3, 2, 1, and 0 are the dome geometry of unit F obtained from the sequential restorations of units A, B, C, D, E, and F, respectively. Accordingly, the profiles display geometry of the dome at the following geologic times: 6 = present time, 5 = 89 Ma, 4 = 112 Ma, 3 = 136 Ma, 2 = 141 Ma, and 1 = 154 Ma.
The restorations indicate that the dome structure began its main phase of development in the Late Cretaceous (stages 4 and 5) and then continued to grow to its present structure (stage 6). Prior to the Late Cretaceous, profiles 1, 2, and 3 show that the structure was composed of several small amplitude culminations that were not localized at the position of the subsequent dome crest. The profiles also show small local structures interpreted as flexures that developed in the proximity of faults. The restoration lacks sufficient temporal resolution to determine if these features are fault drag folds or, alternatively, formed as folds that were subsequently cut by faults.
Faulting of the Sedimentary Cover
In addition to recovering folding, the restoration method that we applied also sequentially restored fault offsets. We focused the analysis on three faults out of the seven included in the geomodel and structural restorations (Figure 6). These three faults are the largest in size and, hence, record the longest history of development. As illustrated in displacement profiles (Figure 6), fault motion began in the Jurassic, prior to the development of the dome in the Cretaceous. Moreover, slip prior to dome development shows local maxima that do not coincide with the center of the dome. The faults continued to develop after the Jurassic period contemporaneously with the dome development. However, the displacement patterns and magnitudes on the faults show different patterns after the initiation of dome development. Specifically, maximum displacements generally shifted toward the center of the dome. Parts of some displacement profiles also show small reverse movements, suggesting that parts of the normal fault displacements were partially inverted by folding related to dome formation.
 Figure 6. Evolution of faults computed from the three-dimensional sequential restorations. (A) Map view of the faults. The displacement profiles of faults (B) F1, (C) F2, and (D) F3. Profiles are numbered to indicate deformation stages 6, 5, 4, 3, 2, and 1 obtained from the restorations of units A, B, C, D, E, and F, respectively. Profiles show fault displacements at relative geologic times as follows: 6 = present time, 5 = 89 Ma, 4 = 112 Ma, 3 = 136 Ma, 2 = 141 Ma, and 1 = 154 Ma. The fault profiles were produced by defining points (at nodes of tetrahedra) along the faults corresponding to the cutoffs of unit F that were displaced through restoration (Figure 5A). Mirrored points are connected via lines (vectors) parallel to the fault planes, such that these vectors equal the fault displacements after each restoration step.
Figure 6. Evolution of faults computed from the three-dimensional sequential restorations. (A) Map view of the faults. The displacement profiles of faults (B) F1, (C) F2, and (D) F3. Profiles are numbered to indicate deformation stages 6, 5, 4, 3, 2, and 1 obtained from the restorations of units A, B, C, D, E, and F, respectively. Profiles show fault displacements at relative geologic times as follows: 6 = present time, 5 = 89 Ma, 4 = 112 Ma, 3 = 136 Ma, 2 = 141 Ma, and 1 = 154 Ma. The fault profiles were produced by defining points (at nodes of tetrahedra) along the faults corresponding to the cutoffs of unit F that were displaced through restoration (Figure 5A). Mirrored points are connected via lines (vectors) parallel to the fault planes, such that these vectors equal the fault displacements after each restoration step.
Fault 1 is considered to be the master fault because it has the greatest displacements, which reach around 300 m (984 ft) at the center of the structure (Figure 5B). Most of the displacement on fault 1 took place between profiles 1 and 3, corresponding to Jurassic to Early Cretaceous time. Fault 1 continued to grow with relatively smaller displacements during the Late Cretaceous and Cenozoic periods (see profiles 4, 5, and 6). Fault 2 also exhibits the greatest displacement in Jurassic time, with its most rapid growth between profiles 2 and 3. This was followed by minor amounts of reverse slip in the following development stages. This late-stage reverse fault slip is not consistent with traditional views of faulting styles in this structural setting. However, we suggest that it was likely driven by flexural movements and was localized by the relay zones between the three faults (faults 1, 2, and 3) at the dome center. Fault 3 evolved with fault 1 in the same style but acted as an antithetic fault forming a relatively asymmetrical graben system. The fault displacement profile has two distinct maxima, with the western tip of the fault beyond the geomodel.
DISCUSSION
Salt Deformation
The motion of the salt body is not directly incorporated in our restoration but can be inferred from the structures developed in the cover strata. The primary activity of the faults prior to the formation of the Cretaceous dome is indicative of reactive salt movement (Figure 7) (Vendeville and Jackson, 1992). Specifically, we propose that the normal faults and associated graben formed because of local extension of the cover section. This local extension was possibly driven by regional salt motion and subsidence. However, given that this faulting occurred during the Jurassic and Early Cretaceous, when the sediment cover was relatively flat (see profiles 1, 2, and 3 in Figure 5), the faulting was not initially driven by dome formation. This interpretation is also consistent with the fault traces in a map view, which does not show a radial pattern around the dome. Instead, the faults developed in a general east–west orientation that presumably reflected the regional stress orientations within the sedimentary cover. In contrast, the complete radial distributions of normal faults are commonly documented from areas of active salt diapirism (e.g., Yin and Groshong, 2007).
 Figure 7. Example of experimental models (Vendeville and Jackson 1992, used with permission of Elsevier) used to explain reactive diapirism. Experiments after (A) 2 cm (0.79 in.) (2 h), (B) 3 cm (1.18 in.) (3 h), and (C) 5 cm (1.96 in.) (5 h) of total extension. The black substratum is viscous, which is less dense than its overburden. The uppermost white layer of uneven thickness is postkinematic.
Figure 7. Example of experimental models (Vendeville and Jackson 1992, used with permission of Elsevier) used to explain reactive diapirism. Experiments after (A) 2 cm (0.79 in.) (2 h), (B) 3 cm (1.18 in.) (3 h), and (C) 5 cm (1.96 in.) (5 h) of total extension. The black substratum is viscous, which is less dense than its overburden. The uppermost white layer of uneven thickness is postkinematic.
We cannot directly resolve the nature of the contact between the salt and the faults because of the deterioration of the seismic imaging with depth. Thus, we are unable to assess whether the salt pierced the overlying sediments or the faults offset the top of the salt. The modern dome is, however, low amplitude (gentle) in terms of bed dips and general curvature, as shown in profile 6 in Figure 5. The development of a gently flexed dome suggests that the salt may be in a form of a pillow or low-relief diapir that localized in the region of the preexisting faults. Given the long time of the growth and modest amplitude, the dome grew slowly, driven by either separate or continuous pulses from moving salt. We cannot exclude the possibility that the salt has gone through subtle phases of rise and withdrawal that are beyond the temporal resolution of our model. Furthermore, the dome profiles show that the current geometry of the dome (red profiles) is not perfectly symmetric, because equally distal ends of the dome are not at the same elevations. Structural asymmetry was also present during previous time periods (see sections 1 and 2 in Figure 5). We suggest that this asymmetry is at least in part a by-product of the fault development, particularly the development of a graben system in one side of the dome. The graben-bounding faults are visible from the dome profiles of section S1 in Figure 5B.
The salt growth and dome formation that started in the Late Cretaceous and continued in the Cenozoic may have been driven, in part, by the early plate contact between Arabia and Eurasia. The initiation of the two-plate collision took place circa 64 Ma, marked by the end of ophiolite obduction (Berberian and King, 1981). The collision of the plates resulted in the underthrusting of the Arabian plate during the Oligocene, followed by thickening of the Arabian margin and uplift of Zagros during the Miocene (e.g., Mouthereau et al., 2012). Consistent with this view, the dome structure including the strain patterns calculated from our restoration is elongated with a major axis perpendicular to the general northeast–southwest horizontal maximum compressive stress (Shmax) orientation associated with the Zagros compressional regime (Figure 8). While precise early directions of the Zagros compressional regime are uncertain, Shmax has remained at around N20° since the Neogene (e.g., Lacombe et al., 2011; McQuarrie and Van Hinsbergen, 2013).
 Figure 8. Strain maps computed from the structural restoration model. (A) The dilation and (B) the distortions (first and second invariants of the strain tensor, respectively). The strain is cumulative for all stages (1–6) of restoration on the top surface of unit F. Strain patterns are elongated along a northwest–southeast-trending axis, which is normal to the northeast–southwest-trending maximum compressional stress orientation associated with the Arabia–Eurasia collision (Figure 1).
Figure 8. Strain maps computed from the structural restoration model. (A) The dilation and (B) the distortions (first and second invariants of the strain tensor, respectively). The strain is cumulative for all stages (1–6) of restoration on the top surface of unit F. Strain patterns are elongated along a northwest–southeast-trending axis, which is normal to the northeast–southwest-trending maximum compressional stress orientation associated with the Arabia–Eurasia collision (Figure 1).
Model Applications
The results from our applications of the 3-D geomechanical restorations demonstrated the capabilities to recover reasonable kinematic histories for structures that involve salt. We described the restoration results on the structural evolution of unit F, but results from other units can also be demonstrated from the restored model in the same fashion. Unit F records the structural evolution of both the dome and its associated faults spanning the Jurassic to present time. Results also benefit research on the salt tectonics of the eastern region of Arabia, particularly the Jurassic and Cretaceous section, which includes the most prolific hydrocarbon reservoirs in the subsurface of eastern Arabia (e.g., McGillivray and Husseini, 1992). Many hydrocarbon-bearing anticlines developed in the Gulf region during the Cretaceous, despite the different growth mechanisms presented in the literature (e.g., Faqira et al., 2009; McGillivray and Husseini, 1992). Furthermore, the model results can help in the analyses of hydrocarbon migration, charge, and possible reservoir fluid compartmentalization. The models can provide a context for subsequent investigations that aim to understand the mechanisms and pathways of hydrocarbon charge, specifically by providing constraints on the factors of faults, fractures, and capillary pore systems (e.g., Boles et al., 2004; Cartwright et al., 2007).
CONCLUSIONS
We demonstrated how 3-D geomechanical restoration methods could be applied to investigate the tectonic history of a faulted, salt-related dome. Specifically, we applied these techniques to a domal structure that forms a hydrocarbon field located in eastern Arabia. Focusing on the time window from Jurassic to present day, we found that faulting dominated the area in the Jurassic and that faults continued with varying but lesser degrees of activity during the Cretaceous and Cenozoic. A low-amplitude dome formed in the Late Cretaceous, presumably caused by movement of the underlying Hormuz salt. Given that the faulting initiated before the folding, we interpret that the structure formed as a reactive diapir. These results, although not explicitly modeling salt deformation, suggest that 3-D geomechanical restoration methods can be applied to discern viable geometric and kinematic histories of salt-involved structures.
The structure we analyzed is one of many hydrocarbon-bearing anticlines developed in eastern Arabia during the Cretaceous. A range of different growth mechanisms for these structures have been presented in the literature (e.g., Faqira et al., 2009; McGillivray and Husseini, 1992). Restoration results can help to distinguish between these different growth mechanisms and also assist in the analyses of hydrocarbon migration, charge, and possible reservoir fluid compartmentalization.
REFERENCES CITED
Al-Amri, A., 2013, Seismotectonics and seismogenic source zones of the Arabian Platform, in Al Hosani, K., F. Roure, R. Ellison, and S. Lokier, eds., Lithosphere dynamics and sedimentary basins: The Arabian plate and analogues: Berlin, Springer, p. 295–316, doi:10.1007/978-3-642-30609-9_15.
Allmendinger, R. W., 1998, Inverse and forward numerical modeling of trishear fault-propagation folds: Tectonics, v. 17, no. 4, p. 640–656, doi:10.1029/98TC01907.
Alsharhan, A. S., and A. E. M. Nairn, 1997, Sedimentary basins and petroleum geology of the Middle East: Amsterdam, Elsevier, 843 p., doi:10.1016/B978-044482465-3/50000-0.
Bahroudi, A., and H. A. Koyi, 2003, Effect of spatial distribution of Hormuz salt on deformation style in the Zagros fold and thrust belt: An analogue modelling approach: Journal of the Geological Society, v. 160, no. 5, p. 719–733, doi:10.1144/0016-764902-135.
Berberian, M., and G. C. P. King, 1981, Towards a paleogeography and tectonic evolution of Iran: Reply: Canadian Journal of Earth Sciences, v. 18, no. 11, p. 1764–1766, doi:10.1139/e81-163.
Boles, J. R., P. Eichhubl, G. Garven, and J. Chen, 2004, Evolution of a hydrocarbon migration pathway along basin-bounding faults: Evidence from fault cement: AAPG Bulletin, v. 88, no. 7, p. 947–970, doi:10.1306/02090403040.
Bond, C. E., D. Gibbs, Z. K. Shipton, and S. Jones, 2007, What do you think this is? “Conceptual uncertainty” in geoscience interpretation: GSA Today, v. 17, no. 11, p. 4–10, doi:10.1130/GSAT01711A.1.
Callot, J. P., S. Jahani, and J. Letouzey, 2007, The role of pre-existing diapirs in fold and thrust belt development, Chapter 16, in Lacombe, O., J. Lavé, F. Roure, and J. Vergés, eds., Thrust belts and foreland basins. From fold kinematics to hydrocarbon system: Berlin, Springer, p. 309–325, doi:10.1007/978-3-540-69426-7_16.
Cartwright, J., M. Huuse, and A. Aplin, 2007, Seal bypass systems: AAPG Bulletin, v. 91, no. 8, p. 1141–1166, doi:10.1306/04090705181.
Chamberlin, R. T., 1910, The Appalachian folds of central Pennsylvania: Journal of Geology, v. 18, no. 3, p. 228–251, doi:10.1086/621722.
Dahlstrom, C. D. A., 1969, Balanced cross sections: Canadian Journal of Earth Sciences, v. 6, no. 4, p. 743–757, doi:10.1139/e69-069.
de Santi, M. R., J. L. E. Campos, and L. F. Martha, 2003, 3-D geological restoration using a finite element approach: Gocad Proceedings: 23rd Gocad Meeting, Association Scientifique pour la Geologie et ses Applications, p. 1–12.
Durand-Riard, P., G. Caumon, and P. Muron, 2010, Balanced restoration of geological volumes with relaxed meshing constraints: Computers & Geosciences, v. 36, p. 441–452, doi:10.1016/j.cageo.2009.07.007.
Durand-Riard, P., J. H. Shaw, A. Plesch, and G. Lufadeju, 2013, Enabling 3D geomechanical restoration of strike- and oblique-slip faults using geological constraints, with applications to the deep-water Niger Delta: Journal of Structural Geology, v. 48, p. 33–44, doi:10.1016/j.jsg.2012.12.009.
Edgell, H., 1991, Proterozoic salt basins of the Persian Gulf area and their role in hydrocarbon generation: Precambrian Research, v. 54, no. 1, p. 1–14, doi:10.1016/0301-9268(91)90065-I.
Erslev, E. A., 1991, Trishear fault-propagation folding: Geology, v. 19, no. 6, p. 617–620, doi:10.1130/0091-7613(1991)019<0617:TFPF>2.3.CO;2.
Faqira, M., M. Rademakers, and A. M. Afifi, 2009, New insights into the Hercynian orogeny, and their implications for the Paleozoic hydrocarbon system in the Arabian plate: GeoArabia, v. 14, no. 3, p. 199–228.
Gibbs, A. D., 1983, Balanced cross-section construction from seismic sections in areas of extensional tectonics: Journal of Structural Geology, v. 5, no. 2, p. 153–160, doi:10.1016/0191-8141(83)90040-8.
Gratier, J.-P., and B. Guillier, 1993, Compatibility constraints on folded and faulted strata and calculation of total displacement using computational restoration (UNFOLD program): Journal of Structural Geology, v. 15, no. 3–5, p. 391–402, doi:10.1016/0191-8141(93)90135-W.
Griffiths, P., S. Jones, N. Salter, F. Schaefer, R. Osfield, and H. Reiser, 2002, A new technique for 3-D flexural-slip restoration: Journal of Structural Geology, v. 24, no. 4, p. 773–782, doi:10.1016/S0191-8141(01)00124-9.
Guzofski, C. A., J. P. Mueller, J. H. Shaw, P. Muron, D. A. Medwedeff, F. Bilotti, and C. Rivero, 2009, Insights into the mechanisms of fault-related folding provided by volumetric structural restorations using spatially varying mechanical constraints: AAPG Bulletin, v. 93, no. 4, p. 479–502, doi:10.1306/11250807130.
Kent, P. E., 1958, Recent studies of south Persian salt plugs: AAPG Bulletin, v. 42, no. 12, p. 2951–2972, doi:10.1306/0BDA5C2D-16BD-11D7-8645000102C1865D.
Kent, P. E., 1979, The emergent Hormuz salt plugs of (Zagros mountains), Southern Iran: Journal of Petroleum Geology, v. 2, no. 2, p. 117–144, doi:10.1111/j.1747-5457.1979.tb00698.x.
Konert, G., M. Afifi, S. A. Al-Hajri, and H. J. Droste, 2001, Paleozoic stratigraphy and hydrocarbon habitat of the Arabian plate: GeoArabia, v. 6, p. 407–442.
Lacombe, O., N. Bellahsen, and F. Mouthereau, 2011, Fracture patterns in the Zagros Simply Folded Belt (Fars, Iran): Constraints on early collisional tectonic history and role of basement faults: Geological Magazine, v. 148, p. 940–963, doi:10.1017/S001675681100029X.
Lepage, F., 2003, Génération de maillages tridimensionnels pour la simulation des phénomènes physiques en géosciences, Ph.D. thesis, Institut National Polytechnique de Lorraine, Nancy, France, 254 p.
Li, Y., D. Jia, A. Plesch, J. Hubbard, J. H. Shaw, and M. Wang, 2013, 3-D geomechanical restoration and paleomagnetic analysis of fault-related folds: An example from the Yanjinggou anticline, southern Sichuan Basin: Journal of Structural Geology, v. 54, p. 199–214, doi:10.1016/j.jsg.2013.06.009.
Lovely, P., E. Flodin, C. Guzofski, F. Maerten, and D. D. Pollard, 2012, Pitfalls among the promises of mechanics-based restoration: Addressing implications of unphysical boundary conditions: Journal of Structural Geology, v. 41, p. 47–63, doi:10.1016/j.jsg.2012.02.020.
Maerten, L., and F. Maerten, 2006, Chronologic modeling of faulted and fractured reservoirs using geomechanically based restoration: Technique and industry applications: AAPG Bulletin, v. 90, no. 8, p. 1201–1226, doi:10.1306/02240605116.
Mallet, J.-L., 1992, Discrete smooth interpolation in geometric modelling: Computer Aided Design, v. 24, no. 4, p. 178–191, doi:10.1016/0010-4485(92)90054-E.
McGillivray, J. G., and M. I. Husseini, 1992, The Paleozoic petroleum geology of central Arabia: AAPG Bulletin, v. 76, p. 1473–1490, doi:10.1306/BDFF8A1A-1718-11D7-8645000102C1865D.
McQuarrie, N., and D. J. J. Van Hinsbergen, 2013, Retrodeforming the Arabia-Eurasia collision zone: Age of collision versus magnitude of continental subduction: Geology, v. 41, no. 3, p. 315–318, doi:10.1130/G33591.1.
Moretti, I., F. Lepage, and M. Guiton, 2006, KINE3D: A new 3D restoration method based on a mixed approach linking geometry and geomechanics: Oil & Gas Science and Technology, v. 61, no. 2, p. 277–289, doi:10.2516/ogst:2006021.
Mouthereau, F., O. Lacombe, and J. Vergés, 2012, Building the Zagros collisional orogen: Timing, strain distribution and the dynamics of Arabia/Eurasia plate convergence: Tectonophysics, v. 532-535, p. 27–60, doi:10.1016/j.tecto.2012.01.022.
Mueller, J. P., C. Guzofski, C. Rivero, J. H. Shaw, P. Muron, and F. Bilotti, 2005, New approaches to 3D structural restoration in fold-and-thrust belts using growth strata (abs.): AAPG Annual Meeting Program, Calgary, Alberta, accessed November 3, 2015, http://www.searchanddiscovery.com/abstracts/html/2005/annual/abstracts/mueller.htm.
Muron, J.-P., J.-L. Mallet, and D. A. Medwedeff, 2005, 3D sequential structural restoration: Geometry and kinematics (abs.): AAPG Annual Meeting Program, Calgary, Alberta, accessed November 3, 2015, http://www.searchanddiscovery.com/abstracts/html/2005/annual/abstracts/muron.htm.
Papadrakakis, M., 1981, A method for the automatic evaluation of the dynamic relaxation parameters: Computer Methods in Applied Mechanics and Engineering, v. 25, no. 1, p. 35–48, doi:10.1016/0045-7825(81)90066-9.
Plesch, A., J. H. Shaw, and D. Kronman, 2007, Mechanics of low-relief detachment folding in the Bajiaochang field, Sichuan Basin, China: AAPG Bulletin, v. 91, no. 11, p. 1559–1575, doi:10.1306/06200706072.
Powers, R. W., L. F. Ramirez, C. D. Redmond, and E. L. J. Elberg, 1966, Geology of the Arabian Peninsula sedimentary geology of Saudi Arabia: U.S. Geological Survey Professional Paper 560-D, 154 p.
Rouby, D., H. Xiao, and J. Suppe, 2000, 3-D restoration of complexly folded and faulted surfaces using multiple unfolding mechanisms: AAPG Bulletin, v. 84, no. 6, p. 805–829, doi:10.1306/A9673400-1738-11D7-8645000102C1865D.
Rowan, M. G., and R. A. Ratliff, 2012, Cross-section restoration of salt-related deformation: Best practices and potential pitfalls: Journal of Structural Geology, v. 41, p. 24–37, doi:10.1016/j.jsg.2011.12.012.
Searle, M., and J. Cox, 1999, Tectonic setting, origin, and obduction of the Oman ophiolite: Geological Society of America Bulletin, v. 111, no. 1, p. 104–122, doi:10.1130/0016-7606(1999)111<0104:TSOAOO>2.3.CO;2.
Sharland, P. R., R. Archer, D. M. Casey, R. B. Davies, S. H. Hall, A. P. Heward, A. D. Horbury, and M. D. Simmons, 2013, Arabian plate sequence stratigraphy: GeoArabia Special Publication 2, 371 p.
Shaw, J. H., S. C. Hook, and J. Suppe, 1994, Structural trend analysis by axial surface mapping: AAPG Bulletin, v. 78, no. 5, p. 700–721, doi:10.1306/A25FE38D-171B-11D7-8645000102C1865D.
Talbot, C. J., 1998, Extrusions of Hormuz salt in Iran: London, Geological Society of London Special Publications 143, p. 315–334, doi:10.1144/GSL.SP.1998.143.01.21.
Talbot, C. J., and R. J. Jarvis, 1984, Age, budget and dynamics of an active salt extrusion in Iran: Journal of Structural Geology, v. 6, no. 5, p. 521–533, doi:10.1016/0191-8141(84)90062-2.
Vendeville, B. C., and M. P. A. Jackson, 1992, The rise of diapirs during thin-skinned extension: Marine and Petroleum Geology, v. 9, p. 354–371, doi:10.1016/0264-8172(92)90048-J.
Williams, G. D., S. J. Kane, T. S. Buddin, and A. J. Richards, 1997, Restoration and balance of complex folded and faulted rock volumes: Flexural flattening, jigsaw fitting and decompaction in three dimensions: Tectonophysics, v. 273, no. 3-4, p. 203–218, doi:10.1016/S0040-1951(96)00282-X.
Yin, H., and R. H. Groshong, 2007, A three-dimensional kinematic model for the deformation above an active diapir: AAPG Bulletin, v. 91, no. 3, p. 343–363, doi:10.1306/10240606034.
Ziegler, M. A., 2001, Late Permian to Holocene paleofacies evolution of the Arabian plate and its hydrocarbon occurrences: GeoArabia, v. 6, no. 3, p. 445–504.
Zienkiewicz, O. C., R. L. Taylor, and J. Z. Zhu, 2005, The finite element method: Its basis and fundamentals, 6th ed.: Oxford, Elsevier, 733 p.
AUTHORS
Mohammed M. Al-Fahmi is currently pursuing a Ph.D. in earth sciences at the University of Oxford, United Kingdom. He worked as a geologist for Saudi Aramco, immediately after his graduation in 2004 with a B.S. degree in earth sciences from King Abdulaziz University. His work experience includes geomodeling of rock fractures, structural geology, and hydrocarbon reservoir characterization and simulation. He obtained an M.S. degree in geosciences from the University of Massachusetts Amherst in 2012. He was also a visiting scholar with the Structural Geology Group of Harvard University in 2012.
Andreas Plesch is a research associate in the Structural Geology and Earth Resources Group in the Earth and Planetary Science Department at Harvard University. He received an M.S. degree in geology from State University of New York, Albany (1994), and his Ph.D. from the Free University Berlin, Germany (1999). His research interests involve three-dimensional modeling and analysis of contractional structures on the reservoir to mountain belt scale using a variety of methods with a focus on quantitative aspects and interpretation of seismic reflection data. He has been able to work on structures worldwide, commonly in cooperation with industry partners.
John H. Shaw is the Harry C. Dudley Professor of Structural and Economic Geology and Chair of the Earth and Planetary Sciences Department at Harvard University. He leads an active research program in structural geology and geophysics, with emphasis on petroleum exploration and production methods. He received a Ph.D. from Princeton University in structural geology and applied geophysics and was employed as a senior research geoscientist at Texaco’s Exploration and Production Technology Department in Houston, Texas. Shaw’s research interests include complex trap and reservoir characterization in fold-and-thrust belts and deepwater passive margins. He heads the Structural Geology and Earth Resources Program at Harvard, an industry–academic consortium that supports student research in petroleum systems.
John C. Cole is currently lead geoscientist at Sasol Canada. John has over 30 years of experience in exploration and development with several major oil and gas companies including Texaco, BP, Saudi Aramco, and Repsol USA. He obtained an M.Sc. degree from Imperial College, United Kingdom, in 1980. His educational background is in structural geology and rock mechanics, and over the years he has developed expertise in geocellular modeling, carbonate reservoir characterization, and fracture characterization and modeling.
ACKNOWLEDGMENTS
We thank Saudi Aramco for funding this project and for giving us the technical review and permission to publish the results. We highly appreciate the contributions made by numerous members from the managerial and technical staff of the Reservoir Characterization Department. The authors performed the project at Harvard University and appreciate the support of the Department of Earth and Planetary Sciences.