The AAPG/Datapages Combined Publications Database
AAPG Bulletin
Full Text
![]() Click to view page images in PDF format.
Click to view page images in PDF format.
AAPG Bulletin, V.
DOI: 10.1306/0130191516517255
Subseismic pathway prediction by three-dimensional structural restoration and strain analysis based on  seismic
seismic interpretation
interpretation
 seismic
seismic interpretation
interpretation
Jennifer Ziesch,1 David C. Tanner,2 and Charlotte M. Krawczyk3
1Leibniz Institute for Applied Geophysics, Hannover, Germany; present address: State Authority for Mining, Energy and Geology, Hannover, Germany; [email protected]
2Leibniz Institute for Applied Geophysics, Hannover, Germany; [email protected]
3Leibniz Institute for Applied Geophysics, Hannover, Germany; Technical University of Berlin, Berlin, Germany; Helmholtz Centre Potsdam, Research Centre for Geosciences (GFZ), Potsdam, Germany; [email protected]
ABSTRACT
For both  modeling
modeling and management of a reservoir, pathways to and through the seal into the overburden are of vital importance. Therefore, we suggest applying the presented structural
and management of a reservoir, pathways to and through the seal into the overburden are of vital importance. Therefore, we suggest applying the presented structural  modeling
modeling workflow that analyzes internal strain, elongation, and paleogeomorphology of the given volume. It is assumed that the magnitude of strain is a proxy for the intensity of subseismic scale fracturing. Zones of high strain may correlate with potential migration pathways. Because of the enhanced need for securing near-surface layer integrity when CO2 storage is needed, an interpretation of three-dimensional (3-D)
workflow that analyzes internal strain, elongation, and paleogeomorphology of the given volume. It is assumed that the magnitude of strain is a proxy for the intensity of subseismic scale fracturing. Zones of high strain may correlate with potential migration pathways. Because of the enhanced need for securing near-surface layer integrity when CO2 storage is needed, an interpretation of three-dimensional (3-D)  seismic
seismic data from the Cooperative Research Centre for Greenhouse Gas Technologies Otway site, Australia, was undertaken. The complete 3-D model was retrodeformed. Compaction- plus deformation-related strain was calculated for the whole volume. The strain distribution after 3-D restoration showed a tripartition of the study area, with the most deformation (30%–50%) in the southwest. Of 24 faults, 4 compartmentalize different zones of deformation. The paleomorphology of the seal formation is determined to tilt northward, presumably because of a much larger normal fault to the north. From horizontal extension analysis, it is evident that most deformation occurred before 66 Ma and stopped abruptly because of the production of oceanic crust in the Southern Ocean. Within the seal horizon, various high-strain zones and therefore subseismic pathways were determined. These zones range in width from 50 m (164 ft) up to 400 m (1312 ft) wide and do not simply follow fault traces, and—most importantly—none of them continue into the overburden. Such information is relevant for reservoir management and public communication and to safeguard near-surface ecologic assets.
data from the Cooperative Research Centre for Greenhouse Gas Technologies Otway site, Australia, was undertaken. The complete 3-D model was retrodeformed. Compaction- plus deformation-related strain was calculated for the whole volume. The strain distribution after 3-D restoration showed a tripartition of the study area, with the most deformation (30%–50%) in the southwest. Of 24 faults, 4 compartmentalize different zones of deformation. The paleomorphology of the seal formation is determined to tilt northward, presumably because of a much larger normal fault to the north. From horizontal extension analysis, it is evident that most deformation occurred before 66 Ma and stopped abruptly because of the production of oceanic crust in the Southern Ocean. Within the seal horizon, various high-strain zones and therefore subseismic pathways were determined. These zones range in width from 50 m (164 ft) up to 400 m (1312 ft) wide and do not simply follow fault traces, and—most importantly—none of them continue into the overburden. Such information is relevant for reservoir management and public communication and to safeguard near-surface ecologic assets.
INTRODUCTION
The prediction of subseismic scale faults is important for the management and exploration of reservoirs and their overburden. Such faults have significant effects on permeability and on fluid flow (Antonellini and Aydin, 1994). Many authors have shown that the quantification of the extension from  seismic
seismic interpretation underestimates the true extension because many faults and fractures are likely to be too small to be resolved on a
interpretation underestimates the true extension because many faults and fractures are likely to be too small to be resolved on a  seismic
seismic scale (e.g., Marrett and Allmendinger, 1992; Reston and McDermott, 2014). Although
scale (e.g., Marrett and Allmendinger, 1992; Reston and McDermott, 2014). Although  seismic
seismic -scale faults have displacements between 1 km (3281 ft) and 10 m (33 ft) and borehole core-scale faults have displacements between 1 mm (0.05 in.) and 10 cm (4 in.) (Needham et al., 1996), the scales from 10 cm (4 in.) to 10 m (33 ft) are not resolvable by geophysical exploration methods.
-scale faults have displacements between 1 km (3281 ft) and 10 m (33 ft) and borehole core-scale faults have displacements between 1 mm (0.05 in.) and 10 cm (4 in.) (Needham et al., 1996), the scales from 10 cm (4 in.) to 10 m (33 ft) are not resolvable by geophysical exploration methods.
In the framework of geologic storage of CO2, our project, Prediction of Deformation to Ensure Carbon Traps (PROTECT), aims to predict subseismic scale faults and fractures within the reservoir and the overburden (Krawczyk et al., 2011, 2015). Studies on the geologic storage of CO2 have either concentrated on the reservoir itself (e.g., Chadwick et al., 2004; Riding, 2006) or aquifers close to surface (Norden, 2011), but evaluation of the complete overburden and reservoir is rare (Keating et al., 2014; Krawczyk et al., 2015). For instance, the In-Salah project in central Algeria integrated numerous methods, such as three-dimensional (3-D)  seismic
seismic data, satellite imaging, and seismologic studies (e.g., Mathieson et al., 2010; Stork et al., 2014), as well as various
data, satellite imaging, and seismologic studies (e.g., Mathieson et al., 2010; Stork et al., 2014), as well as various  modeling
modeling techniques, such as static geologic models, multiphase flow models, fracture-flow models, and geomechanical models (e.g., Ringrose et al., 2013), to determine small-scale faulting. These results were used to support operational decisions, but none of these models included subseismic scale fractures. In the Sleipner field (Norway), well log and cuttings,
techniques, such as static geologic models, multiphase flow models, fracture-flow models, and geomechanical models (e.g., Ringrose et al., 2013), to determine small-scale faulting. These results were used to support operational decisions, but none of these models included subseismic scale fractures. In the Sleipner field (Norway), well log and cuttings,  seismic
seismic attribute analysis, geomechanical
attribute analysis, geomechanical  modeling
modeling , and time-lapse gravity surveys have been carried out to make sure that the CO2 plume is not migrating into the overburden (Chadwick et al., 2004; Eiken et al., 2011). In the International Energy Agency Weyburn Project (central Canada), which is one of the largest enhanced oil recovery–carbon capture and storage (CCS) projects, numerous methods, such as time-lapse 3-D
, and time-lapse gravity surveys have been carried out to make sure that the CO2 plume is not migrating into the overburden (Chadwick et al., 2004; Eiken et al., 2011). In the International Energy Agency Weyburn Project (central Canada), which is one of the largest enhanced oil recovery–carbon capture and storage (CCS) projects, numerous methods, such as time-lapse 3-D  seismic
seismic , reservoir simulations, geochemical
, reservoir simulations, geochemical  modeling
modeling , regional geoscience investigations, and wellbore integrity studies, were applied to characterize the reservoir and overburden (Whittaker et al., 2011). However, as Eiken et al. (2011) noted, dynamic
, regional geoscience investigations, and wellbore integrity studies, were applied to characterize the reservoir and overburden (Whittaker et al., 2011). However, as Eiken et al. (2011) noted, dynamic  modeling
modeling is a challenge and there is still room for further model improvement.
is a challenge and there is still room for further model improvement.
Project PROTECT combined  seismic
seismic multiattributes (Trappe and Hellmich, 2003; Krawczyk et al., 2015), forward
multiattributes (Trappe and Hellmich, 2003; Krawczyk et al., 2015), forward  modeling
modeling (Aruffo et al., 2014), and 3-D retrodeformation results. The project cooperates with Australia’s first demonstration site of deep geologic storage of CO2 in the Otway Basin (southwestern Victoria, Australia; Cook, 2014). This paper is primarily concerned with the 3-D retrodeformation of the interpretation of high-quality 3-D
(Aruffo et al., 2014), and 3-D retrodeformation results. The project cooperates with Australia’s first demonstration site of deep geologic storage of CO2 in the Otway Basin (southwestern Victoria, Australia; Cook, 2014). This paper is primarily concerned with the 3-D retrodeformation of the interpretation of high-quality 3-D  seismic
seismic data (Ziesch et al., 2017) and the internal strain that occurred as a consequence of restoration. The calculated strain results are used as a proxy to predict the location of subseismic scale fractures and therefore potential CO2 migration pathways. The insights pertaining to the 3-D retrodeformation method used here can be potentially implemented in a number of applications, especially subsurface storage or exploitation.
data (Ziesch et al., 2017) and the internal strain that occurred as a consequence of restoration. The calculated strain results are used as a proxy to predict the location of subseismic scale fractures and therefore potential CO2 migration pathways. The insights pertaining to the 3-D retrodeformation method used here can be potentially implemented in a number of applications, especially subsurface storage or exploitation.
GEOLOGIC SETTING
The study area (∼8 km [∼5 mi]  ∼7 km [∼4 mi]) is located in southwestern Victoria, 200 km (125 mi) southwest of Melbourne, Australia (Figure 1). It is part of the onshore western Otway Basin, an extensional basin that developed along the southern margin of Australia during the Late Jurassic because of the separation of Australia and Antarctica (Watson et al., 2004). In the mid-Late Cretaceous the tectonic setting changed to compressional deformation with associated uplift and fault inversion (Norvick and Smith, 2001). After a 2.5-m.y. hiatus, the last deformation phase began with fast continental spreading in the Southern Ocean during the Lutetian (41 Ma; Lawver et al., 2011) coupled with thermal subsidence and marine transgression. Previous faults were reactivated under northeast-southwest extension (Norvick and Smith, 2001), in combination with syntectonic deposition. The faults imaged in the
∼7 km [∼4 mi]) is located in southwestern Victoria, 200 km (125 mi) southwest of Melbourne, Australia (Figure 1). It is part of the onshore western Otway Basin, an extensional basin that developed along the southern margin of Australia during the Late Jurassic because of the separation of Australia and Antarctica (Watson et al., 2004). In the mid-Late Cretaceous the tectonic setting changed to compressional deformation with associated uplift and fault inversion (Norvick and Smith, 2001). After a 2.5-m.y. hiatus, the last deformation phase began with fast continental spreading in the Southern Ocean during the Lutetian (41 Ma; Lawver et al., 2011) coupled with thermal subsidence and marine transgression. Previous faults were reactivated under northeast-southwest extension (Norvick and Smith, 2001), in combination with syntectonic deposition. The faults imaged in the  seismic
seismic data were all formed during the first phase of deformation and were still active during the third phase (Ziesch et al., 2017).
data were all formed during the first phase of deformation and were still active during the third phase (Ziesch et al., 2017).
 Figure 1. Overview map of the regional tectonics, showing major normal faults in the Otway Basin (compiled from Douglas and Ferguson, 1988; Alley and Lindsay, 1995; Perincek and Cockshell, 1995; Moore et al., 2000). Cretaceous sedimentary rocks marked in gray. Close-up of the study area, showing borehole locations (Cooperative Research Centre [CRC]-1, -2) and the traces of the profiles (0–9) used for the extension versus age diagram (Figure 11). Major fault is marked.
Figure 1. Overview map of the regional tectonics, showing major normal faults in the Otway Basin (compiled from Douglas and Ferguson, 1988; Alley and Lindsay, 1995; Perincek and Cockshell, 1995; Moore et al., 2000). Cretaceous sedimentary rocks marked in gray. Close-up of the study area, showing borehole locations (Cooperative Research Centre [CRC]-1, -2) and the traces of the profiles (0–9) used for the extension versus age diagram (Figure 11). Major fault is marked.
The stratigraphy of the study area can be divided into eight supersequences that are combined here as five lithostratigraphic groups; they are as follows, from oldest to youngest: the Otway, Sherbrook, Wangerrip, Nirranda, and Heytesbury Groups (Figure 2; Tupper et al., 1993). The stratigraphic horizons interpreted in the  seismic
seismic volume belong to the youngest four of the five groups (Figure 2). The Otway Group consists of fluvial-lacustrine sedimentary rocks that accumulated during the first rifting phase and are overlain by the Sherbrook Group, which contains an alternating sequence of sandstones and mudstones. The Sherbrook Group includes the reservoir (Waarre Formation [Fm.]) and seals (Flaxman Fm., Belfast Mudstone (Mst.), and Skull Creek Mst.) for CO2 storage. The beginning of the passive margin sedimentation is represented by the Wangerrip Group, which consists of 700 m (2297 ft) of sandstones and mudstones (Norvick and Smith, 2001; Krassay et al., 2004). After a major hiatus of 8.5 m.y., the Nirranda Group was deposited in proximal and distal environments (Norvick and Smith, 2001). Fine-grained facies of the Narrawaturk Marl overlay sandstones of the thin Mepunga Fm. The Miocene Heytesbury Group was deposited under full marine conditions and is characterized by limestones and marls (Krassay et al., 2004).
volume belong to the youngest four of the five groups (Figure 2). The Otway Group consists of fluvial-lacustrine sedimentary rocks that accumulated during the first rifting phase and are overlain by the Sherbrook Group, which contains an alternating sequence of sandstones and mudstones. The Sherbrook Group includes the reservoir (Waarre Formation [Fm.]) and seals (Flaxman Fm., Belfast Mudstone (Mst.), and Skull Creek Mst.) for CO2 storage. The beginning of the passive margin sedimentation is represented by the Wangerrip Group, which consists of 700 m (2297 ft) of sandstones and mudstones (Norvick and Smith, 2001; Krassay et al., 2004). After a major hiatus of 8.5 m.y., the Nirranda Group was deposited in proximal and distal environments (Norvick and Smith, 2001). Fine-grained facies of the Narrawaturk Marl overlay sandstones of the thin Mepunga Fm. The Miocene Heytesbury Group was deposited under full marine conditions and is characterized by limestones and marls (Krassay et al., 2004).
 Figure 2. Stratigraphy of the study area, modified after Ziesch et al. (2017), compiled from Perincek and Cockshell (1995) and Geoscience Australia and Australian Stratigraphy Commission (2017). The key horizons picked in the three-dimensional
Figure 2. Stratigraphy of the study area, modified after Ziesch et al. (2017), compiled from Perincek and Cockshell (1995) and Geoscience Australia and Australian Stratigraphy Commission (2017). The key horizons picked in the three-dimensional  seismic
seismic data set are shown, as are the ranges of thicknesses between the horizons in parentheses. Fm. = Formation; Mst. = Mudstone; Quat. = Quaternary; Sst. = Sandstone.
data set are shown, as are the ranges of thicknesses between the horizons in parentheses. Fm. = Formation; Mst. = Mudstone; Quat. = Quaternary; Sst. = Sandstone.
Ziesch et al. (2017) presented depth and isochore maps of all the horizons in the study area. Figure 3 shows concise summary maps of the reservoir and seal horizons (i.e., Turonion top Waarre Fm. and Santonian top Skull Creek Mst., respectively). Vertical displacements on faults increase from northeast to southwest, where throws up to 800 m (2625 ft) can be observed (Figure 3A, D). Relay ramps act as soft-linking elements between the major faults. Fault Buttress Southeast and fault 6 form a horst structure; between these two faults, a major change in stratigraphic thickness occurs. In general, the thicknesses increase for both stratigraphic horizons toward the southwest and the normal faults were strongly synsedimentary (Figure 3B, E).
 Figure 3. Maps of the two stratigraphic horizons: top Waarre Formation (Fm.) and top Skull Creek Mudstone (Mst.) (modified after Ziesch et al., 2017, and used with permission of Wiley): (A) Depth map of top Waarre Fm. (B) Isochore map of top Waarre Fm. to top Skull Creek Mst. It shows strong fault growth and an increase in thickness toward the southwest. (C) Structural map of top Waarre Fm.; fault heave polygons are shown in white. Black arrows represent the average dip direction, and gray arrows indicate the directions of cylindricity vectors of the faults. See text for details. (D) Depth map of Skull Creek Mst. (E) Isochore map of Skull Creek Mst. to top Timboon Sst. Similar to the underlaying formation, the faults show strong growth thicknesses and the sedimentary thickness increases toward the southwest. (F) Structural map of top Skull Creek Mst. Fault heave polygons are shown in white. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
Figure 3. Maps of the two stratigraphic horizons: top Waarre Formation (Fm.) and top Skull Creek Mudstone (Mst.) (modified after Ziesch et al., 2017, and used with permission of Wiley): (A) Depth map of top Waarre Fm. (B) Isochore map of top Waarre Fm. to top Skull Creek Mst. It shows strong fault growth and an increase in thickness toward the southwest. (C) Structural map of top Waarre Fm.; fault heave polygons are shown in white. Black arrows represent the average dip direction, and gray arrows indicate the directions of cylindricity vectors of the faults. See text for details. (D) Depth map of Skull Creek Mst. (E) Isochore map of Skull Creek Mst. to top Timboon Sst. Similar to the underlaying formation, the faults show strong growth thicknesses and the sedimentary thickness increases toward the southwest. (F) Structural map of top Skull Creek Mst. Fault heave polygons are shown in white. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
DATABASE AND METHOD
The database is a  seismic
seismic volume (32.3 km [20.1 mi]
volume (32.3 km [20.1 mi]  14.35 km [8.92 mi]
14.35 km [8.92 mi]  4.1 s two-way time) with a 24-fold bin size of 20
4.1 s two-way time) with a 24-fold bin size of 20  20 m (66
20 m (66  66 ft). The data were acquired and processed in 2000 (Cooperative Research Centre for Greenhouse Gas Technologies, 2013, personal communication). The used signal frequency range was 5–90 Hz, and the recorded offset range was 28 to 2280 m (92 to 7480 ft). The 3-D poststack finite-difference time migration was used for imaging.
66 ft). The data were acquired and processed in 2000 (Cooperative Research Centre for Greenhouse Gas Technologies, 2013, personal communication). The used signal frequency range was 5–90 Hz, and the recorded offset range was 28 to 2280 m (92 to 7480 ft). The 3-D poststack finite-difference time migration was used for imaging.
Because the target depth of the data acquisition geometry was the Turonian Waarre Fm. reservoir (∼1.6-km [∼1-mi] depth), the uppermost 400 m (1312 ft) of the data set are less well-imaged compared with the rest of the volume. The reflections of the seal and the overburden formations are well imaged (Figure 4). In total, 8 stratigraphic horizons (including the reservoir, seal, and overburden) and 24 major faults were interpreted in the time domain (Ziesch et al., 2017; Figure 4).
 Figure 4. Perspective view of the three-dimensional
Figure 4. Perspective view of the three-dimensional  seismic
seismic data with two inlines, one crossline, and a variance depth slice. The rear inline shows interpretation of eight stratigraphic horizons; the crossline shows interpretation of the faults; the front inline section is not interpreted. Fm. = Formation.
data with two inlines, one crossline, and a variance depth slice. The rear inline shows interpretation of eight stratigraphic horizons; the crossline shows interpretation of the faults; the front inline section is not interpreted. Fm. = Formation.
For time–depth conversion, interval velocities were determined from sonic velocities measured in the injection well Cooperative Research Centre-1. This information was used to generate velocity gradients for each stratigraphic formation. Quality control of the velocity model relied on nine wells in the larger  seismic
seismic volume (for more information, see Ziesch et al., 2017).
volume (for more information, see Ziesch et al., 2017).
Structural  Modeling
Modeling Workflow
Workflow
The deformation analysis required several model building and  modeling
modeling steps (Figure 5). After importing the depth-converted horizons and faults into the structural
steps (Figure 5). After importing the depth-converted horizons and faults into the structural  modeling
modeling software, individual fault blocks were defined (Figure 5). This involved separating the stratigraphic horizons along the major faults. This step was important because it was necessary to be able to move each fault block separately.
software, individual fault blocks were defined (Figure 5). This involved separating the stratigraphic horizons along the major faults. This step was important because it was necessary to be able to move each fault block separately.
 Figure 5. Workflow used in this study. After
Figure 5. Workflow used in this study. After  seismic
seismic interpretation and model building, the uppermost horizon was decompacted and the next top formation was restored. This procedure was repeated until the restoration of the lowest formation. This generates values of incremental elongation, the paleogeomorphology, and distribution of the internal strain within the fault blocks. 3-D = three-dimensional.
interpretation and model building, the uppermost horizon was decompacted and the next top formation was restored. This procedure was repeated until the restoration of the lowest formation. This generates values of incremental elongation, the paleogeomorphology, and distribution of the internal strain within the fault blocks. 3-D = three-dimensional.
Tetrahedral volumes were built for each fault block between stratigraphic horizons (Figure 6A). The magnitude of strain was calculated by the change in position of all vertices in the tetrahedron relative to their initial, undeformed state (La Pointe et al., 2002; Figure 6B, C).
 Figure 6. Example of tetrahedral volumes. (A) Excerpt from the volume model with one fault between two fault blocks; (B) unstrained tetrahedron with a sphere of unity radius; and (C) strained tetrahedron with a strain ellipsoid and its principal strain axes
Figure 6. Example of tetrahedral volumes. (A) Excerpt from the volume model with one fault between two fault blocks; (B) unstrained tetrahedron with a sphere of unity radius; and (C) strained tetrahedron with a strain ellipsoid and its principal strain axes  , where e is the strain value.
, where e is the strain value.
A two-step approach was used for retrodeformation. First, the uppermost horizon was backstripped; after this, the next top formation was restored, from southwest to northeast. In the following, the methods of decompaction and restoration are explained in detail.
Backstripping and Decompaction
Deposition of younger sedimentary rocks on older strata causes compaction. Thus, the first step during retrodeformation is the sequential removal of the overlying stratigraphic formation and decompacting the underlying sedimentary rocks (Figure 5). Backstripping results in each being compensated for their new position by using the porosity of the formations at depth and the constant c (Table 1). This is derived using Athy’s equation
where φ is the porosity at depth y (km), c is a constant (km−1), and 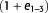 is the initial porosity (Athy, 1930). In this way, the compaction of sedimentary rocks can be attributed to only two parameters, c and
is the initial porosity (Athy, 1930). In this way, the compaction of sedimentary rocks can be attributed to only two parameters, c and 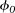 (Table 1).
(Table 1).

Porosity was derived from a shale volume log 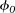 . The average
. The average 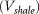 value for each stratigraphic horizon was determined, assuming the percentage of material that is not shale is coarser, that is, silt and sand. Parameters for all the interpreted units were calculated using standard values of c and
value for each stratigraphic horizon was determined, assuming the percentage of material that is not shale is coarser, that is, silt and sand. Parameters for all the interpreted units were calculated using standard values of c and 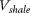 for shale and sandstone (Sclater and Christie, 1980).
for shale and sandstone (Sclater and Christie, 1980).
Decompaction is a purely vertical process. Faults were included in this process and retrodeformed to their uncompacted dip; that is, in general, the fault dip becomes steeper after each backstripping and decompaction stage (Durand-Riard et al., 2011).
Restoration
The term “restoration” means that a cross section or map is restored back to its undeformed state. This requires accounting for deformation related to tectonic events (Durand-Riard et al., 2011; Chauvin et al., 2015). Since the last century, structural balancing of cross sections has been used to check the consistency of the geologic interpretation (e.g., Chamberlin, 1910; Dahlstrom, 1969; Gibbs, 1983). However, the transfer of structural balancing into the third dimension has been practiced only for the last two decades (e.g., Rouby et al., 2000; Guzofski et al., 2009; Durand-Riard et al., 2011) and will become increasingly important with the increased availability of 3-D  seismic
seismic data. Retrodeformation of a geologic 3-D model offers new analytical options: the differing amounts of extension throughout the model, the 3-D paleogeomorphology, and the 3-D internal strain that occurred within the retrodeformed fault block volumes (Figure 5).
data. Retrodeformation of a geologic 3-D model offers new analytical options: the differing amounts of extension throughout the model, the 3-D paleogeomorphology, and the 3-D internal strain that occurred within the retrodeformed fault block volumes (Figure 5).
The complete 3-D model of the study area, including 24 faults and 8 horizons, was restored back into the undeformed state, from southwest to northeast that is, the northeastern edge of the study area was kept fixed during restoration. The reason for this strategy was that the study area is part of the passive margin between southern Australia and Antarctica (Williamson et al., 1990): major faults dip and become younger toward the southwest. All underlying formations were also passively restored during the structural restoration of the top horizon.
The 3-D retrodeformation raises some new challenges with respect to two-dimensional (2-D) restoration.
• Fault shape: in three dimensions, the fault surface can vary laterally (i.e., fault corrugations) and with respect to depth (e.g., listric faults).
• Displacement: faults show variable displacements along strike until the tip point is reached and the displacement approaches zero.
• Fault kinematics: the 3-D movement vector on the fault surface, can be difficult to extract in three dimensions (Ziesch et al., 2015). We calculated mean 3-D kinematic vectors for the faults by using the cylindricity of corrugations of the fault surface (for more information, see Ziesch et al., 2017), but in reality, the faults can have slightly variable kinematic vectors along strike. Only a few degrees difference can lead to an uneven retrodeformed surface.
Compaction Strain versus Deformation Strain
Strain is caused by compaction and structural deformation. With retrodeformation, the strain caused by decompaction and restoration is the reciprocal of the forward strain tensor and therefore a proxy for subseismic scale fractures. This retrodeformation strain can be differentiated into strain by compaction and strain by deformation. It can be expressed by a finite strain ellipsoid (Figure 6) with three principal axes of finite strain with semiaxis lengths: 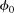 (Ramsay and Huber, 1983).
(Ramsay and Huber, 1983).
An initially circular (spherical) marker is transformed during purely vertical decompaction and compaction to a finite strain ellipse (ellipsoid) (Figure 7). Compaction causes uniaxial compression so the resulting finite strain ellipse (ellipsoid) has a shorter  axis but a constant
axis but a constant  axis. For instance, there is a reduction of 53%
axis. For instance, there is a reduction of 53% 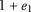 magnitude after a 53% bulk volume loss (Figure 7A).
magnitude after a 53% bulk volume loss (Figure 7A).
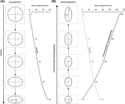 Figure 7. Schematic diagram showing the development of strain during compaction and decompaction. (A) Compaction history over time during which a circle with a unit radius undergoes deformation. The resulting finite strain ellipse is characterized by a shorter
Figure 7. Schematic diagram showing the development of strain during compaction and decompaction. (A) Compaction history over time during which a circle with a unit radius undergoes deformation. The resulting finite strain ellipse is characterized by a shorter 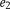 axis and a constant
axis and a constant 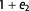 axis, where
axis, where 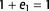 are the principal strain axes and e is the strain value. The graph shows the relationship of
are the principal strain axes and e is the strain value. The graph shows the relationship of 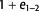 magnitude over time. (B) The reverse of (A) to show the effect of decompaction;
magnitude over time. (B) The reverse of (A) to show the effect of decompaction; 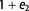 from the finite compaction stage is the reciprocal of
from the finite compaction stage is the reciprocal of 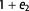 from the finite decompaction stage.
from the finite decompaction stage.
The  seismic
seismic interpretation represents the compacted, present-day state. The model was backstripped and decompacted to the original predeformation state to analyze the compaction-related strain. As
interpretation represents the compacted, present-day state. The model was backstripped and decompacted to the original predeformation state to analyze the compaction-related strain. As 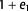 in the finite compaction stage is equal to
in the finite compaction stage is equal to 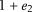 in the finite decompaction stage, decompaction strain is directly related to compaction strain.
in the finite decompaction stage, decompaction strain is directly related to compaction strain.
Strain caused by faulting can be differentiated into rotation and shearing. Forward deformation of an initially circular (spherical) marker with a shear angle of 90° in the hanging wall of a listric fault will lead to a sheared and rotated finite strain ellipse (ellipsoid) (Figure 8A). However, the geologic interpretation represents the deformed present-day state. By structural restoring of the hanging wall, it is possible to analyze the strain tensors in all tetrahedra of the hanging wall (Figure 6), thereby investigating the distribution of volumetric strain. With respect to the forward deformation, the ellipsoid’s axes caused by structural restoring are mirrored around the vertical axis, but the 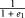 -strain magnitude correlates with the equivalent forward deformation
-strain magnitude correlates with the equivalent forward deformation  -strain magnitude (Figure 8B).
-strain magnitude (Figure 8B).
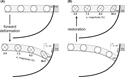 Figure 8. Development of internal strain during structural restoration. (A) Forward deformation with a shear angle of 90° in the hanging wall (HW) of a listric fault using inclined shear. The circle undergoes both rotation and shear. (B) The geologic model of the study area represents the deformed present-day state. By restoring the HW, one is able to analyze the
Figure 8. Development of internal strain during structural restoration. (A) Forward deformation with a shear angle of 90° in the hanging wall (HW) of a listric fault using inclined shear. The circle undergoes both rotation and shear. (B) The geologic model of the study area represents the deformed present-day state. By restoring the HW, one is able to analyze the  strain magnitude, where
strain magnitude, where  is the principal major strain axis and e is the strain value. The strain ellipse caused by structural restoration has the same magnitudes, but as in forward deformation, their axes, which are mirrored around a vertical axis, include rotation. The angle β is the shear angle. FW = footwall.
is the principal major strain axis and e is the strain value. The strain ellipse caused by structural restoration has the same magnitudes, but as in forward deformation, their axes, which are mirrored around a vertical axis, include rotation. The angle β is the shear angle. FW = footwall.
As in all geologic  modeling
modeling software programs that use volumetric cells, extremely acute angles within the cells, which can be produced in the process of retrodeformation (e.g., during decompaction, behind faults), can cause unnaturally high strain values. In the 3-D model, the faults are corrugated (Ziesch et al., 2015) and the horizon surfaces are tightly faulted; because interpolation and smoothing were avoided, the surfaces appear in the model with an unsmoothed geometry. Because the areas with abnormally high strains can be clearly seen because of their peculiar shape (e.g., circular shape) and location (e.g., directly behind faults), the strain maps are presented here without any modification of this issue and it is addressed in the text so that the readers can judge for themselves.
software programs that use volumetric cells, extremely acute angles within the cells, which can be produced in the process of retrodeformation (e.g., during decompaction, behind faults), can cause unnaturally high strain values. In the 3-D model, the faults are corrugated (Ziesch et al., 2015) and the horizon surfaces are tightly faulted; because interpolation and smoothing were avoided, the surfaces appear in the model with an unsmoothed geometry. Because the areas with abnormally high strains can be clearly seen because of their peculiar shape (e.g., circular shape) and location (e.g., directly behind faults), the strain maps are presented here without any modification of this issue and it is addressed in the text so that the readers can judge for themselves.
Inclined Shear Algorithm
The inclined shear algorithm (also known as simple shear) was chosen for structural restoration (Gibbs, 1983; White et al., 1986) because the faults in the study area are either listric (the dip of the listric faults in the south changes from 60°–70° in the upper parts to 30°–40° in the lower parts, e.g., fault Naylor South or fault Naylor East) or subplanar with a corrugated morphology (e.g., fault Buttress Northwest, Ziesch et al., 2017). The hanging wall of a fault block is moved along a 3-D movement vector (see Table 2). An angle β is chosen, on which shearing will occur in the hanging wall during restoration (Hauge and Gray, 1996). If the dip of the fault in the transport direction changes, simple shear is used to compensate the necessary change in the geometry of the hanging wall. The amount of shearing depends on the change in the dip of the fault in the transport direction. The inclined shear algorithm was first developed for 2-D restoration but is available for 3-D restoration in the structural  modeling
modeling software (Move 2016.2, Midland Valley Exploration Ltd., 2016). However, the inclined shear algorithm should be considered as a 2.5-dimensional or pseudo 3-D solution, because although a 3-D movement vector was used, the inclined shear algorithm divides the 3-D model into 2-D sections parallel to the 3-D vector (Midland Valley Exploration Ltd., 2017, personal communication). In the transport direction, all particles of the hanging wall are displaced with constant heave, but along the fault strike, that is, in the third dimension, the heave amount varies in proportion to the cutoffs of the faulted strata. The method maintains the volume of the hanging wall in 3-D, but it does not maintain bed thickness if shearing occurs (Williams and Vann, 1987).
software (Move 2016.2, Midland Valley Exploration Ltd., 2016). However, the inclined shear algorithm should be considered as a 2.5-dimensional or pseudo 3-D solution, because although a 3-D movement vector was used, the inclined shear algorithm divides the 3-D model into 2-D sections parallel to the 3-D vector (Midland Valley Exploration Ltd., 2017, personal communication). In the transport direction, all particles of the hanging wall are displaced with constant heave, but along the fault strike, that is, in the third dimension, the heave amount varies in proportion to the cutoffs of the faulted strata. The method maintains the volume of the hanging wall in 3-D, but it does not maintain bed thickness if shearing occurs (Williams and Vann, 1987).

 Seismic
Seismic interpretation and variance analysis proved that the faults of the study area possess a distinct morphology and that these subvertical corrugations are real (Ziesch et al., 2017). To quantify the amount and orientations of the corrugations, curvature and cylindricity attributes of the fault surfaces were calculated. The resulting vectors of the cylindricity analysis are shown in Figure 3C. We postulated that the corrugations were generated and maintained during the growth of the synsedimentary faults (Ziesch et al., 2017). Therefore, the corrugation vectors could be used as 3-D movement vectors for each fault in the model (see Table 2; Ziesch et al., 2017, 2015). It was determined that the 3-D movement vectors were either pure dip slip or slightly dextrally oblique slip (gray arrows, Figure 3C). During each restoration step, the same 3-D movement vector was used for each fault.
interpretation and variance analysis proved that the faults of the study area possess a distinct morphology and that these subvertical corrugations are real (Ziesch et al., 2017). To quantify the amount and orientations of the corrugations, curvature and cylindricity attributes of the fault surfaces were calculated. The resulting vectors of the cylindricity analysis are shown in Figure 3C. We postulated that the corrugations were generated and maintained during the growth of the synsedimentary faults (Ziesch et al., 2017). Therefore, the corrugation vectors could be used as 3-D movement vectors for each fault in the model (see Table 2; Ziesch et al., 2017, 2015). It was determined that the 3-D movement vectors were either pure dip slip or slightly dextrally oblique slip (gray arrows, Figure 3C). During each restoration step, the same 3-D movement vector was used for each fault.
The optimum β angle is typically steep, antithetic to the main fault (Schultz-Ela, 1992; Withjack and Peterson, 1993; Hauge and Gray, 1996). To demonstrate the influence of the shear angle on the final restoration, a structural restoration with three different shear angles is shown for one fault block (Figure 9). The amount of strain within the hanging wall and the correctness of restoration depend mostly on the β angle (the precondition is of course a correct  seismic
seismic interpretation). The highest priority is the resulting morphology of the surface, that is, the restored hanging-wall surface should be as smooth as possible and should match the original depositional surface (i.e., the regional). In this example, a shear angle of 55° represents the optimum result with a smooth surface of the hanging wall. This also inherently causes the smallest strain magnitudes within the hanging wall (Figure 9D). Because the dips of the normal faults vary in this model, antithetic shear angles between 45° and 80° were used. The shear angles found to work best for the faults in the study area are listed in Table 2.
interpretation). The highest priority is the resulting morphology of the surface, that is, the restored hanging-wall surface should be as smooth as possible and should match the original depositional surface (i.e., the regional). In this example, a shear angle of 55° represents the optimum result with a smooth surface of the hanging wall. This also inherently causes the smallest strain magnitudes within the hanging wall (Figure 9D). Because the dips of the normal faults vary in this model, antithetic shear angles between 45° and 80° were used. The shear angles found to work best for the faults in the study area are listed in Table 2.
 Figure 9. Examples of oblique inclined shear restoration. The hanging wall (HW) is deformed by penetrative slip planes, using an inclined shear vector with the shear angle β. (A) Unrestored state, (B) β = 85°, (C) β = 75°, (D) β = 55°. The result obtained in (D) clearly shows a smoother top surface and the smallest
Figure 9. Examples of oblique inclined shear restoration. The hanging wall (HW) is deformed by penetrative slip planes, using an inclined shear vector with the shear angle β. (A) Unrestored state, (B) β = 85°, (C) β = 75°, (D) β = 55°. The result obtained in (D) clearly shows a smoother top surface and the smallest 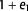 strain values, where
strain values, where  is the principal major strain axis and e is the strain value. β = 55° is the best option for restoration in this example. FW = footwall.
is the principal major strain axis and e is the strain value. β = 55° is the best option for restoration in this example. FW = footwall.
DEFORMATION QUANTIFICATION
Extension Over Time
The 2-D cross section (extracted from the 3-D model, Figure 10A) shows that the Skull Creek Mst. is highly faulted by southwest-dipping normal faults and northeast-dipping, antithetic faults (Ziesch et al., 2017). The first restoration step begins with the last movement, that is, the youngest fault zone. The study area is part of a passive margin rift basin, that is, the sediment depocenters and fault activity both migrated toward the sea-floor spreading center in the south (see also Finlayson et al., 1998). Therefore, it is highly probable that the order of faulting, even in this small area, was from north to south. The restoration of the fault sequence was carried out in the opposite sense. After complete restoration, the length of the retrodeformed Skull Creek Mst. is reduced and the entire restored formation is tilted northward by approximately 5° (Figure 10B).
 Figure 10. The interpreted and retrodeformed Skull Creek Mudstone (Mst.) horizon. (A) The two-dimensional cross section of the deformed Skull Creek Mst.; (B) the same horizon restored and additionally decompacted to the preslip stage. The detailed view shows two restoration steps (vertical exaggeration = 1.5): (C) interpreted horizon with two normal faults, (D) restoration of the hanging wall of the younger, antithetic fault, and (E) restoration of the older synthetic fault. The dashed lines indicate the active objects during movement. Δl = increment of elongation; FP = fixed pin; LP = loose pin.
Figure 10. The interpreted and retrodeformed Skull Creek Mudstone (Mst.) horizon. (A) The two-dimensional cross section of the deformed Skull Creek Mst.; (B) the same horizon restored and additionally decompacted to the preslip stage. The detailed view shows two restoration steps (vertical exaggeration = 1.5): (C) interpreted horizon with two normal faults, (D) restoration of the hanging wall of the younger, antithetic fault, and (E) restoration of the older synthetic fault. The dashed lines indicate the active objects during movement. Δl = increment of elongation; FP = fixed pin; LP = loose pin.
The elongation of the faulted horizons was determined by analyzing 10 2-D cross sections through the 3-D model (for location, see Figure 1), before and after restoration. The extension versus age diagram (Figure 11) illustrates the elongation of the stratigraphic horizons over time. The rate of extension decreased abruptly from top Waarre Fm. to top Narrawaturk Fm. Although the median extension of the Waarre Fm. is 9.2% and that of Skull Creek Mst. is 7.1%, the variation in the extension for the 10 cross sections is up to 12%, i.e., almost twice the median value. After Timboon Sandstone (Sst.) deposition (66 Ma), the total elongation after this point was only approximately 1%. Most extension occurred during the deposition of Skull Creek Mst. and the underlying Waarre Fm., that is, most faults terminated at approximately 66 m.y.a.
 Figure 11. Extension versus age diagram showing the incremental elongation of the 10 cross sections (see locations in Figure 1). The box represents the 25%–75% percentile, and the whiskers represent the minimum and maximum extent. During Late Cretaceous (top Waarre Formation [Fm.] and top Skull Creek Mudstone [Mst.]), the cross sections show median values of 7%–10% extension, but there is a very wide range (see text for details). The deformation activity dies out rapidly after Timboon Sandstone (Sst.) deposition. In all 10 cross sections, 99% of extension occurred before deposition of top Timboon Sst. (66 Ma). After 66 Ma, the elongation was almost only 1%, that is, most faults had died out by this time. Gr. = Group; Mst. = Mudstone.
Figure 11. Extension versus age diagram showing the incremental elongation of the 10 cross sections (see locations in Figure 1). The box represents the 25%–75% percentile, and the whiskers represent the minimum and maximum extent. During Late Cretaceous (top Waarre Formation [Fm.] and top Skull Creek Mudstone [Mst.]), the cross sections show median values of 7%–10% extension, but there is a very wide range (see text for details). The deformation activity dies out rapidly after Timboon Sandstone (Sst.) deposition. In all 10 cross sections, 99% of extension occurred before deposition of top Timboon Sst. (66 Ma). After 66 Ma, the elongation was almost only 1%, that is, most faults had died out by this time. Gr. = Group; Mst. = Mudstone.
Strain Distribution
To better understand the finite retrodeformation strain maps, the different components of compactional strain and deformation strain for the Skull Creek Mst. were separately analyzed. The development of the compaction strain within the Skull Creek Mst. over time is presented in Figure 12. The backstripping of the overburden strata between the topography and the top Mepunga Fm. cause 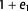 compaction strain magnitudes up to 10% within the Skull Creek Mst. (Figure 12A). The northwestern part of the study area displays slightly higher deformation than the remainder of the study area (Figure 12A). After the backstripping of the Mepunga Fm., the compaction strain increases up to 25% across the area (Figure 12B). Note that because of software limitations, extreme strain values that occur near the faults should not be considered meaningful (the software uses vertical decompaction and calculates therefore unnatural strain in the shadow of the faults; Midland Valley Exploration Ltd., 2016, personal communication). The next backstripping step caused an increase of the strain values by approximately 5% in large areas (Figure 12C). Following the backstripping of the Pebble Point Fm. and Timboon Sst., the compaction strain increases significantly. The southern area now has the highest compaction strain values (Figure 12D).
compaction strain magnitudes up to 10% within the Skull Creek Mst. (Figure 12A). The northwestern part of the study area displays slightly higher deformation than the remainder of the study area (Figure 12A). After the backstripping of the Mepunga Fm., the compaction strain increases up to 25% across the area (Figure 12B). Note that because of software limitations, extreme strain values that occur near the faults should not be considered meaningful (the software uses vertical decompaction and calculates therefore unnatural strain in the shadow of the faults; Midland Valley Exploration Ltd., 2016, personal communication). The next backstripping step caused an increase of the strain values by approximately 5% in large areas (Figure 12C). Following the backstripping of the Pebble Point Fm. and Timboon Sst., the compaction strain increases significantly. The southern area now has the highest compaction strain values (Figure 12D).
 Figure 12. Cumulative strain caused by compaction within the Skull Creek Mudstone (Mst.) calculated by stepwise backstripping of the following overburden strata: (A) between topographical surface and top Mepunga Fm., (B) between top Mepunga and top Dilwyn Fm., (C) between top Dilwyn and top Pebble Point Fm., (D) between top Pebble Point Fm. and top Skull Creek Mst. (see Figure 2). See text for more information about strain artifacts. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
Figure 12. Cumulative strain caused by compaction within the Skull Creek Mudstone (Mst.) calculated by stepwise backstripping of the following overburden strata: (A) between topographical surface and top Mepunga Fm., (B) between top Mepunga and top Dilwyn Fm., (C) between top Dilwyn and top Pebble Point Fm., (D) between top Pebble Point Fm. and top Skull Creek Mst. (see Figure 2). See text for more information about strain artifacts. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
The deformation strain within the Skull Creek Mst. is shown at different restoration steps (Figure 13). The color-coded maximum  strain magnitude increases southward and ranges from 0% to approximately 75% (Figure 13). A total of 16 restoration steps were performed (Figure 13D), which corresponds to the number of faults that were restored. Four faults are a major factor; they are as follows: fault 16, fault Naylor South, fault Buttress Northwest, and fault 2, because the
strain magnitude increases southward and ranges from 0% to approximately 75% (Figure 13). A total of 16 restoration steps were performed (Figure 13D), which corresponds to the number of faults that were restored. Four faults are a major factor; they are as follows: fault 16, fault Naylor South, fault Buttress Northwest, and fault 2, because the  strain is significantly unequally distributed between these structures. In general, the Skull Creek Mst. can be divided into two parts: the southern part underwent much more deformation than the northern area (Figure 13D). In Figure 13C and D, stripe features can be observed. These features are related to the fault corrugations (see Discussion section). They do not reflect the strain orientation; rather, they only reflect zones of high strain magnitudes.
strain is significantly unequally distributed between these structures. In general, the Skull Creek Mst. can be divided into two parts: the southern part underwent much more deformation than the northern area (Figure 13D). In Figure 13C and D, stripe features can be observed. These features are related to the fault corrugations (see Discussion section). They do not reflect the strain orientation; rather, they only reflect zones of high strain magnitudes.
 Figure 13. Maps of the deformation strain (
Figure 13. Maps of the deformation strain ( strain magnitudes, where e is the strain value and
strain magnitudes, where e is the strain value and  is the principal major strain axis) after three-dimensional (3-D) structural restoration of the Skull Creek Mudstone (Mst.). The faults causing the tripartition are labeled. (A) Unrestored Skull Creek Mst.; fault heave polygons are shown in white. (B) First intermediate step up to fault 16 and fault Naylor South. (C) second intermediate step after restoration up to fault Buttress Northwest (NW) and fault 2. (D) complete 3-D structural restoration of the Skull Creek Mst. See text for more information about stripe artifacts. Dashed line shows profile location of section in Figure 16. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
is the principal major strain axis) after three-dimensional (3-D) structural restoration of the Skull Creek Mudstone (Mst.). The faults causing the tripartition are labeled. (A) Unrestored Skull Creek Mst.; fault heave polygons are shown in white. (B) First intermediate step up to fault 16 and fault Naylor South. (C) second intermediate step after restoration up to fault Buttress Northwest (NW) and fault 2. (D) complete 3-D structural restoration of the Skull Creek Mst. See text for more information about stripe artifacts. Dashed line shows profile location of section in Figure 16. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
Decompaction and restoration together determine the finite strain. The results after backstripping of the overburden and subsequent 3-D structural restoration of the Skull Creek Mst. are shown in Figure 14. The background strain is the compaction strain that occurred within the Skull Creek Mst. over the complete approximately 80 m.y. The northern area has 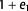 strain values between 12% and 25%, whereas the central and southern part has slightly higher pre-Skull Creek Mst. deformation strain. After the restoring of all fault blocks, the strain is significantly inhomogeneously distributed (Figure 14, similar to Figure 13).
strain values between 12% and 25%, whereas the central and southern part has slightly higher pre-Skull Creek Mst. deformation strain. After the restoring of all fault blocks, the strain is significantly inhomogeneously distributed (Figure 14, similar to Figure 13).
 Figure 14. Maps of the
Figure 14. Maps of the  strain magnitudes, where e is the strain value and
strain magnitudes, where e is the strain value and  is the principal major strain axis, after decompaction and subsequent three-dimensional (3-D) structural restoration of the Skull Creek Mudstone (Mst.). The
is the principal major strain axis, after decompaction and subsequent three-dimensional (3-D) structural restoration of the Skull Creek Mudstone (Mst.). The 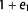 strain magnitude is color-coded and represents the cumulative strain from both decompaction and structural restoration. The faults causing the tripartition are labeled. (A) Unrestored Skull Creek Mst. after decompaction and structural restoration of the overburden. (B) First intermediate step up to fault 16 and fault Naylor South. (C) Second intermediate step after retrodeformation up to fault Buttress Northwest (NW) and fault 2. (D) Complete 3-D retrodeformation of the Skull Creek Mst. grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
strain magnitude is color-coded and represents the cumulative strain from both decompaction and structural restoration. The faults causing the tripartition are labeled. (A) Unrestored Skull Creek Mst. after decompaction and structural restoration of the overburden. (B) First intermediate step up to fault 16 and fault Naylor South. (C) Second intermediate step after retrodeformation up to fault Buttress Northwest (NW) and fault 2. (D) Complete 3-D retrodeformation of the Skull Creek Mst. grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
The combination of compaction and deformation strain offers a more detailed subdivision: the strain north of fault Buttress Northwest and fault 2 is, in comparison to the other areas, mostly from deposition of the overburden and not from tectonics. In contrast, the southern part is strongly deformed, mostly because of tectonic movement. The central area between fault Naylor South and fault 16 in the south and fault Buttress Northwest and fault 2 in the north underwent intermediate amounts of deformation.
DISCUSSION
From 3-D retrodeformation analysis, it is possible to infer paleogeomorphology, elongation rate, and subseismic scale strain that occurred within the faulted blocks of geologic formations. Comparative studies are rare (e.g., Mohr et al., 2005; Lohr et al., 2008; Freeman et al., 2015). Most case studies analyzed the structural style, fault growth, and fault population of  seismic
seismic -scale faults (e.g., Needham et al., 1996; Mansfield and Cartwright, 2001; Nicol et al., 2005; Tvedt et al., 2013), but subseismic scale faults and fractures are commonly not considered. For the first time, both the seismically visible faults (Ziesch et al., 2017) and, in this paper, the prediction of the location of subseismic scale structures are evaluated in the context of a CCS project.
-scale faults (e.g., Needham et al., 1996; Mansfield and Cartwright, 2001; Nicol et al., 2005; Tvedt et al., 2013), but subseismic scale faults and fractures are commonly not considered. For the first time, both the seismically visible faults (Ziesch et al., 2017) and, in this paper, the prediction of the location of subseismic scale structures are evaluated in the context of a CCS project.
Paleogeomorphology
After decompaction and structural restoration of the 3-D geologic model, the complete Skull Creek Mst. is tilted northward (Figure 10B). Typically, a stratigraphic horizon is tilted by faulting, for instance, if the fault is nonplanar. Extensional movement on a listric fault can generate a roll-over anticline (Williams and Vann, 1987) or block rotation can be caused by domino-style faulting on a planar fault. Therefore, it is proposed that the study area was probably part of the hanging wall of a much larger normal fault (Figure 15). This major fault is located in the north of the study area and counts as one of the biggest faults of the onshore Otway Basin (for location, see Figure 1). However, thickening of any sedimentary units toward the northeast was not observed, in fact, the opposite is the case. The study area is too far from the major fault (∼20 km [∼12 mi]) to observe this feature. Activity on this major fault probably led to tilting of the Skull Creek Mst. The fault was only active prior to the end of Skull Creek Mst. deposition because, after this time, the retrodeformed beds are no longer tilted.
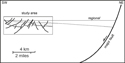 Figure 15. Schematic diagram showing an interpretation to explain the northward-tilt of the restored Skull Creek Mudstone. The area was probably affected by a major fault (see Figure 1 for location) outside the study area, to the north.
Figure 15. Schematic diagram showing an interpretation to explain the northward-tilt of the restored Skull Creek Mudstone. The area was probably affected by a major fault (see Figure 1 for location) outside the study area, to the north.
 Figure 16. Two-dimensional cross sections of the retrodeformed Skull Creek Mudstone (Mst.) and Timboon Sandstone (Sst.) with their respective strain distributions and interpretations (for location of cross section, see Figure 13D). The
Figure 16. Two-dimensional cross sections of the retrodeformed Skull Creek Mudstone (Mst.) and Timboon Sandstone (Sst.) with their respective strain distributions and interpretations (for location of cross section, see Figure 13D). The  strain magnitude, where e is the strain value and
strain magnitude, where e is the strain value and  is the principal major strain axis, is color-coded. (A) Timboon Sst.: the
is the principal major strain axis, is color-coded. (A) Timboon Sst.: the 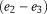 strain magnitude is close to zero, except for the southernmost tip. (B) Sketch showing the amount of subseismic scale fracturing is minimal. (C) Skull Creek Mst.: the
strain magnitude is close to zero, except for the southernmost tip. (B) Sketch showing the amount of subseismic scale fracturing is minimal. (C) Skull Creek Mst.: the  strain magnitudes are higher in the southwestern and central parts. (D) Sketch showing the relative distribution of the subseismic scale faults in the Skull Creek Mst. Areas with patches of higher strain magnitudes (violet). These areas are potential pathways for fluid or gas migration, but subseismic scale fractures of the underlain Skull Creek Mst. do not continue into the Timboon Sst. above.
strain magnitudes are higher in the southwestern and central parts. (D) Sketch showing the relative distribution of the subseismic scale faults in the Skull Creek Mst. Areas with patches of higher strain magnitudes (violet). These areas are potential pathways for fluid or gas migration, but subseismic scale fractures of the underlain Skull Creek Mst. do not continue into the Timboon Sst. above.
Elongation Rate
The analysis of extension over time shows that the largest variation in the amount of total extension is between top Waarre and top Timboon (Figure 11). The average horizontal extension rate within the study area during the Late Cretaceous was 0.36% per m.y., which corresponds to approximately 0.028 mm/yr (∼0.001 in./yr). This is very small, compared with the extension rates of other passive margins (>3.5 mm/yr [0.1 in./yr]; Brune et al., 2014). The extension rate of the study area does not, however, reflect the extension rate of the whole Otway Basin, which would require the analysis of the complete passive margin.
Most deformation occurred during the Cretaceous and stopped at the beginning of the Paleocene. The abrupt stop of extension at 66 Ma, which is associated with the absence of faults, represents the transition from synrift to postrift in this area and is probably caused by the start of the production of true oceanic crust in the Southern Ocean (Blevin and Cathro, 2008). This marks the relaxation of the extensional stress field in the Otway Basin and the northern passive margin as a whole (see discussion in White et al. (2013)).
Subseismic Scale Strain
The distribution of strain within a 3-D geologic model is of special interest because this is important for the prediction of the location of potential leakage pathways (e.g., Lohr et al., 2008; Krawczyk and Tanner, 2010; Watkins et al., 2015, 2018). Walsh and Watterson (1992) estimated the number of subseismic scale faults using a fractal method. However, this method assumes that subseismic scale fractures exist homogeneously throughout a volume. Other authors have attempted to predict fracture density from outcrop or  seismic
seismic surfaces by using curvature or the azimuthal amplitude versus offset method, albeit sometimes with conflicting results (Lisle, 1994; Hunt et al., 2010; Suo et al., 2012). The approach taken in this paper is to kinematically restore each fault and thereby assess the strain that occurs within each hanging-wall volume. We postulate that the magnitude and distribution of the strain in the hanging wall after restoration is a proxy for the amount and distribution of subseismic scale deformation (Plesch et al., 2007; Lohr et al., 2008). This deformation, above a certain magnitude, is probably manifested as subseismic scale fracturing. According to van der Pluijm and Marshak (2004), brittle fracturing occurs at finite strains of approximately 5%. However, this model could not be calibrated with, for example, formation microimager (FMI) data from boreholes (as carried out by, for instance, Lohr et al., 2008), and therefore the amount of strain calculated in the 3-D retrodeformation is treated here in a relative manner, that is, we postulate that high amounts of modeled deformation correlate with a large density of subseismic scale fracturing. The amount of subseismic scale fracturing can be evaluated by interrogating the
surfaces by using curvature or the azimuthal amplitude versus offset method, albeit sometimes with conflicting results (Lisle, 1994; Hunt et al., 2010; Suo et al., 2012). The approach taken in this paper is to kinematically restore each fault and thereby assess the strain that occurs within each hanging-wall volume. We postulate that the magnitude and distribution of the strain in the hanging wall after restoration is a proxy for the amount and distribution of subseismic scale deformation (Plesch et al., 2007; Lohr et al., 2008). This deformation, above a certain magnitude, is probably manifested as subseismic scale fracturing. According to van der Pluijm and Marshak (2004), brittle fracturing occurs at finite strains of approximately 5%. However, this model could not be calibrated with, for example, formation microimager (FMI) data from boreholes (as carried out by, for instance, Lohr et al., 2008), and therefore the amount of strain calculated in the 3-D retrodeformation is treated here in a relative manner, that is, we postulate that high amounts of modeled deformation correlate with a large density of subseismic scale fracturing. The amount of subseismic scale fracturing can be evaluated by interrogating the 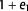 strain magnitude of the tetrahedra that make up the hanging wall (e.g., Lohr et al., 2008; Krawczyk et al., 2015). The finite strain tensor within a stratigraphic volume is composed of strain caused by differential compaction and strain caused by tectonic deformation.
strain magnitude of the tetrahedra that make up the hanging wall (e.g., Lohr et al., 2008; Krawczyk et al., 2015). The finite strain tensor within a stratigraphic volume is composed of strain caused by differential compaction and strain caused by tectonic deformation.
The calculated, uniaxial, compaction-related deformation is a proxy for the amount of volume loss (Isaacs, 1981). The results show that the presently 2.2-km (7217-ft)-deep Skull Creek Mst. has minimum compaction strain values of 15%. The southern part is slightly more compacted (20%–22%) than the northeastern area (Figure 12). This could have resulted in higher compaction-related flattening of the fault surfaces, which are more listric in the south. This is a similar observation to that of the theoretical discussion in Jones and Addis (1984).
The strain results of the structural restoration within the Skull Creek Mst. show, at 30%–50%, higher values in the southwest than in the northeast (Figure 13D). The differences in strain along fault strike are probably caused by fault morphology. In addition, the fault surfaces are irregularly corrugated. The corrugations are subparallel to the dip direction of the faults, and they have widths of 100–500 m (328–1640 ft) and lengths of 500–2750 m (1640–9022 ft), that is, above  seismic
seismic resolution (Ziesch et al., 2017). They are mostly not continuous along the length of the faults, although the breaks are not related to a particular strata. Therefore, when restoring, even parallel to the corrugation direction of the faults, the irregularity of the fault surface reveals internal strain in the hanging wall. The amount of subseismic scale deformation is postulated to be dependent on the amplitude of the corrugations because regions with higher strain correlate with more corrugations of the fault surfaces (Figure 13B–D). All geologic formations underwent more deformation in areas where the fault corrugations are more prominent. Similar to these results, Lohr et al. (2008) observed in the Northwest German Basin that the deformation of the hanging wall is strongly controlled by the fault morphology. The highest strain areas were connected to strong changes in fault strike or fault dip.
resolution (Ziesch et al., 2017). They are mostly not continuous along the length of the faults, although the breaks are not related to a particular strata. Therefore, when restoring, even parallel to the corrugation direction of the faults, the irregularity of the fault surface reveals internal strain in the hanging wall. The amount of subseismic scale deformation is postulated to be dependent on the amplitude of the corrugations because regions with higher strain correlate with more corrugations of the fault surfaces (Figure 13B–D). All geologic formations underwent more deformation in areas where the fault corrugations are more prominent. Similar to these results, Lohr et al. (2008) observed in the Northwest German Basin that the deformation of the hanging wall is strongly controlled by the fault morphology. The highest strain areas were connected to strong changes in fault strike or fault dip.
The Appendix presents forward  modeling
modeling of a hanging-wall volume on fault Buttress Southeast (Figures 17, 18). The forward and retrodeformation results are comparable because the strain tensor is mirrored (Figure 8B). Even by reducing the resolution of the fault grid (Figure 18A), the strain distribution is still comparable. The strain maximums and the strain minimums are located in the same areas. Therefore, we interpret that the fault possesses a basic morphology, with topographic variation above 300 m (984 ft), that causes a basic strain pattern. The corrugations below 300 m (984 ft) produce additional strain that is superimposed on this basic pattern. The distribution of strain does not give information about the orientation of subseismic scale fractures. Figure 18B shows the calculated strike directions of subseismic scale fractures based on the orientation of the strain tensor
of a hanging-wall volume on fault Buttress Southeast (Figures 17, 18). The forward and retrodeformation results are comparable because the strain tensor is mirrored (Figure 8B). Even by reducing the resolution of the fault grid (Figure 18A), the strain distribution is still comparable. The strain maximums and the strain minimums are located in the same areas. Therefore, we interpret that the fault possesses a basic morphology, with topographic variation above 300 m (984 ft), that causes a basic strain pattern. The corrugations below 300 m (984 ft) produce additional strain that is superimposed on this basic pattern. The distribution of strain does not give information about the orientation of subseismic scale fractures. Figure 18B shows the calculated strike directions of subseismic scale fractures based on the orientation of the strain tensor  plane). Note that lineations of high strain magnitude are not parallel to the fracture orientations.
plane). Note that lineations of high strain magnitude are not parallel to the fracture orientations.
 Figure 17. (A) Map showing the location of fault Buttress Southeast (SE). Black box shows the area modeled in Figure 18. (B) Surface of fault Buttress SE; color-coded by curvature (above) and cylindricity (below); insert shows stereographic projection of poles to the surface triangles. (C) Two triangulated fault surfaces of Buttress SE. The lighter blue surface represents the 75-m (246-ft) gridded surface used in this work. The darker green surface represents the 150-m (492-ft) gridded surface. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
Figure 17. (A) Map showing the location of fault Buttress Southeast (SE). Black box shows the area modeled in Figure 18. (B) Surface of fault Buttress SE; color-coded by curvature (above) and cylindricity (below); insert shows stereographic projection of poles to the surface triangles. (C) Two triangulated fault surfaces of Buttress SE. The lighter blue surface represents the 75-m (246-ft) gridded surface used in this work. The darker green surface represents the 150-m (492-ft) gridded surface. Grid coordinate system: Map Grid of Australia, zone 54, Transverse Mercator projection.
 Figure 18. (A) Forward
Figure 18. (A) Forward  modeling
modeling of a planar volume (75 m [246 ft] mesh) along the fault Buttress Southeast at different amounts of movement (100 m [328 ft], 300 m [984 ft], 500 m [1640 ft], and 700 m [2297 ft]). The
of a planar volume (75 m [246 ft] mesh) along the fault Buttress Southeast at different amounts of movement (100 m [328 ft], 300 m [984 ft], 500 m [1640 ft], and 700 m [2297 ft]). The  strain magnitude, where e is the strain value and
strain magnitude, where e is the strain value and  is the principal major strain axis, is color-coded and represents the cumulative strain. The left column represents the 150-m (492-ft) fault grid and the right column represents the 300-m (984-ft) fault grid. (B) Example for the strain map and the resultant strike direction (black lines) of subseismic scale fractures.
is the principal major strain axis, is color-coded and represents the cumulative strain. The left column represents the 150-m (492-ft) fault grid and the right column represents the 300-m (984-ft) fault grid. (B) Example for the strain map and the resultant strike direction (black lines) of subseismic scale fractures.
Because of the complex fault surface morphologies, the best shear angle value for the retrodeformation of each fault was determined separately (Figure 9; Appendix, Table 2). The appropriate shear angle for inclined shear has been the subject of discussion since the early 1980s. Although Groshong and Richard (1989) recommend shear angles that are exactly antithetic to a major fault, Xiao and Suppe (1992) suggested shear orientations for normal faults of 67°, which approximate the Coulomb collapse of deforming materials. The shear angles used in this work fit very well with the suggestion of Xiao and Suppe (1992), especially considering that lateral variation of the fault shape can change the shear angle by up to ±15° (Yamada and McClay, 2003).
The strain occurs as stripe features during restoration. It can be excluded that these are caused by a numerical error because of the mesh density. All surfaces and volumes were manually constructed and checked for integrity (e.g., bad triangles in surfaces and acute angles in tetrahedra; see the quality of the triangulation in the 3-D supplementary PDF in Ziesch et al., 2017). The cause of the strain magnitude stripes are the fault corrugations and their impact on the inclined shear method. Other authors, for instance Lohr et al. (2008) and Watkins et al. (2015, 2018), have shown similar features occur during 3-D restoration using the same software (Move, Midland Valley Exploration Ltd., 2016). However, as Brandes and Tanner (2014) remark, all kinematic models of fault restoration in the present-day are limited because of the use of the same kinematic behavior for every part of the fault (instead of a combination of different algorithms) and the still rudimentary application of originally 2-D algorithms in the third dimension.
After the combination of decompaction and subsequent 3-D restoration of the Skull Creek Mst., the study area has a strongly deformed (55%–80%) southern part, a medium deformed (25%–55%) central area between the four major faults, and the northern area is less deformed (10%–25%; Figure 14D). The tripartition of the study area supports the hypothesis of a hierarchical system of normal faults. Although 24 normal and antithetic faults were defined as major faults (based on fault length and throw), these 4 faults acted as higher-order master faults (see also Needham et al., 1996; Watterson et al., 1996). They are the biggest faults in the study area; they have the largest lengths (in the strike direction) and offsets up to 800 m (2625 ft).
It is noticeable that, particularly in the areas of relays (Figure 3C, F), more subseismic scale deformation occurred (Figure 13A; e.g., fault 10, fault Naylor South). Ziesch et al. (2017) observed torsion of the relays at the depth of the Skull Creek Mst. By retrodeforming the complete model, including the relays, the amount of additional deformation that the relays underwent is made apparent (see Figure 14D).
The detailed analysis of subseismic scale deformation within the complete overburden provides insight into potential pathways. These could significantly influence the flow of CO2, hydrocarbons, or hydrothermal fluids. To better illustrate this, Figure 16 shows a 2-D section (for location, see Figure 13D) through the decompacted and restored Skull Creek Mst. and Timboon Fm. The 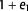 strain magnitude within the stratigraphic formations is used as a proxy to evaluate the location of potential migration pathways (Lohr et al., 2008). Strain by compaction is uniaxial and therefore not taken into account. We propose that parts of the study area with
strain magnitude within the stratigraphic formations is used as a proxy to evaluate the location of potential migration pathways (Lohr et al., 2008). Strain by compaction is uniaxial and therefore not taken into account. We propose that parts of the study area with  strain magnitudes over 2%–3% are potential areas of subseismic scale faulting, and therefore point to pathways of potential fluid or gas migration.
strain magnitudes over 2%–3% are potential areas of subseismic scale faulting, and therefore point to pathways of potential fluid or gas migration.
The  strain magnitude within the overlying Timboon Fm. is close to zero, which means that within this and also all other overburden formations, the amount of subseismic scale fracturing is minimal. Even if the model was increased to the north, using available data, which is not presented here, this effect would still be observed. Therefore, subseismic scale fracturing does not continue beyond the seal formation into higher stratigraphic formations. Within the higher stratigraphy, only seismically visible faults could be pathways. Thus, the retrodeformation method is able to locate possible critical areas of subseismic scale fracturing (Figure 16). Validation as to whether these fractures and therefore pathways are sealing or not could not be accomplished. However, in a case study of an inverted fault in the Northwest Germany Basin, Lohr et al. (2008) showed that strain shown by 3-D retrodeformation correlates well with the results of FMI data from boreholes within the hanging wall, that is, there was a positive correlation between the amount of strain and the amount of fractures determined by FMI.
strain magnitude within the overlying Timboon Fm. is close to zero, which means that within this and also all other overburden formations, the amount of subseismic scale fracturing is minimal. Even if the model was increased to the north, using available data, which is not presented here, this effect would still be observed. Therefore, subseismic scale fracturing does not continue beyond the seal formation into higher stratigraphic formations. Within the higher stratigraphy, only seismically visible faults could be pathways. Thus, the retrodeformation method is able to locate possible critical areas of subseismic scale fracturing (Figure 16). Validation as to whether these fractures and therefore pathways are sealing or not could not be accomplished. However, in a case study of an inverted fault in the Northwest Germany Basin, Lohr et al. (2008) showed that strain shown by 3-D retrodeformation correlates well with the results of FMI data from boreholes within the hanging wall, that is, there was a positive correlation between the amount of strain and the amount of fractures determined by FMI.
The subseismic scale deformation in the Otway Basin occurred coevally with the Cretaceous sedimentation. Isochore maps showed that nearly all faults are growth faults at different stratigraphic levels, that is, strong fault growth occurred during movement on the faults. Therefore, shortly after deposition, the partially consolidated Skull Creek sedimentary rocks were deformed. Because the rocks were still close to the surface, the sediment φ was approximately 40%–45%. It is likely that, because of increased fluid flow at this time, mineral precipitation occurred within the fractures.
SUMMARY AND CONCLUSIONS
For the first time in the Otway Basin, a 3-D structural restoration and strain analysis of a geologic model of a storage reservoir was carried out. This paper shows the following.
• The compaction-related deformation increases with depth up to approximately 30% volume loss.
• The study area is controlled by four major faults, where the highest strain values occur in the southwestern part of the study area. These faults are of a higher hierarchy, that is, they acted as higher-order master faults, with respect to the other 20 major faults.
• Subseismic scale fracturing of the seal horizon (Skull Creek Mst.) occurs and is inhomogeneously distributed.
• Subseismic fracturing does not extend into the overlaying formations.
• Restoration yields a unique understanding of the geologic evolution of the area. The Skull Creek Mst. was northwardly inclined during its deposition because of movement on a major fault outside the study area.
It is concluded that it is possible to retrodeform a complete 3-D model using the workflow presented in this paper to identify the distribution and magnitude of subseismic scale fractures. Strain maps help to predict the relative distribution of fracture density in areas without well data, and thus to predict potential migration pathways. The strain results remain relative until calibration is possible using FMI data or core data.
We recommend that the 3-D retrodeformation method should always be used on baseline data before any subsurface use to determine whether subseismic pathways exist, which are prime structures along which leakage out of a reservoir could occur.
APPENDIX
This appendix deals with the theoretical consideration as to what degree fault corrugations influence strain in the hanging wall. Forward  modeling
modeling is presented for fault Buttress Southeast, which is located in the eastern part of the study area (Figure 17A). In the
is presented for fault Buttress Southeast, which is located in the eastern part of the study area (Figure 17A). In the  seismic
seismic interpretation, the fault surface is characterized by corrugations, which are strong, parallel linear zones of high curvature, see Figure 17B. Ziesch et al. (2015) demonstrated that these corrugations are above
interpretation, the fault surface is characterized by corrugations, which are strong, parallel linear zones of high curvature, see Figure 17B. Ziesch et al. (2015) demonstrated that these corrugations are above  seismic
seismic resolution. To determine the influence of the corrugations on the strain distribution within the hanging wall, the original triangulated fault surface was resampled (direct triangulation, mean approximately 50 m [∼164 ft]) at two coarser regular grid sizes (150 m [492 ft] and 300 m [984 ft]), and forward
resolution. To determine the influence of the corrugations on the strain distribution within the hanging wall, the original triangulated fault surface was resampled (direct triangulation, mean approximately 50 m [∼164 ft]) at two coarser regular grid sizes (150 m [492 ft] and 300 m [984 ft]), and forward  modeling
modeling was carried out on the regular-gridded hanging-wall volume on these fault surfaces. During the forward
was carried out on the regular-gridded hanging-wall volume on these fault surfaces. During the forward  modeling
modeling , the hanging-wall volume was moved stepwise downward every 100 m (328 ft), for a total of 700 m (2297 ft) along the fault surface. The strain distribution in the hanging wall is shown after 100 m (328 ft), 300 m (984 ft), 500 m (1640 ft), and 700 m (2297 ft) (Figure 18A). Figure 18B shows the orientation of the strain tensor after 700-m (2297-ft) movement of the hanging wall on the 150-m (492-ft) gridded fault surface.
, the hanging-wall volume was moved stepwise downward every 100 m (328 ft), for a total of 700 m (2297 ft) along the fault surface. The strain distribution in the hanging wall is shown after 100 m (328 ft), 300 m (984 ft), 500 m (1640 ft), and 700 m (2297 ft) (Figure 18A). Figure 18B shows the orientation of the strain tensor after 700-m (2297-ft) movement of the hanging wall on the 150-m (492-ft) gridded fault surface.
REFERENCES CITED
Alley, N. F., and J. M. Lindsay, 1995, Tertiary, in J. F. Drexel and W. V. Preiss, eds., The geology of South Australia, Volume 2, The Phanerozoic: Adelaide, South Australia, Australia, Geological Survey of South Australia Bulletin 54, p. 150–217.
Antonellini, M., and A. Aydin, 1994, Effect of faulting on fluid flow in porous sandstones: Petrophysical properties: AAPG Bulletin, v. 78, no. 3, p. 355–377.
Aruffo, C. M., A. Rodriguez-Herrera, E. Tenthorey, F. Krzikalla, J. Minton, and A. Henk, 2014, Geomechanical modelling to assess fault integrity at the CO2CRC Otway Project, Australia: Australian Journal of Earth Sciences, v. 61, no. 7, p. 987–1001, doi:10.1080/08120099.2014.958876.
Athy, L. F., 1930, Density, porosity and compaction of sedimentary rocks: AAPG Bulletin, v. 14, no. 1, p. 1–24.
Blevin, J., and D. Cathro, 2008, Australian southern margin synthesis, project GA707: Canberra, Australian Capital Territory, Australia, FrOG Tech Pty. Ltd., 104 p.
Brandes, C., and D. C. Tanner, 2014, Fault-related folding: A review of kinematic models and their application: Earth-Science Reviews, v. 138, p. 352–370, doi:10.1016/j.earscirev.2014.06.008.
Brune, S., C. Heine, M. Pérez-Gussinyé, and S. V. Sobolev, 2014, Rift migration explains continental margin asymmetry and crustal hyper-extension: Nature Communications, v. 5, doi:10.1038/ncomms5014.
Chadwick, R. A., P. Zweigel, U. Gregersen, G. A. Kirby, S. Holloway, and P. N. Johannessen, 2004, Geological reservoir characterization of a CO2 storage site: The Utsira Sand, Sleipner, northern North Sea: Energy, v. 29, no. 9–10, p. 1371–1381, doi:10.1016/j.energy.2004.03.071.
Chamberlin, R. T., 1910, The Appalachian folds of central Pennsylvania: Journal of Geology, v. 18, no. 3, p. 228–251.
Chauvin, B., A. Mazuyer, and G. Caumon, 2015, Mechanics-based restoration: A physical and mathematical review: 35th Gocad Meeting–2015 Research for Integrative Numerical Geology Meeting, Nancy, France, September 22–25, 2015, 34 p.
Cook, P. J., ed., 2014, Geologically storing carbon: Learning from the Otway project experience: Melbourne, Victoria, Australia, CSIRO Publishing, 408 p.
Dahlstrom, C. D. A., 1969, Balanced cross sections: Canadian Journal of Earth Sciences, v. 6, p. 743–757, doi:10.1139/e69-069.
Douglas, J. G., and J. A. Ferguson, eds. 1988, Geology of Victoria: Melbourne, Victoria, Australia, Geological Society of Australia, v. 5, 663 p.
Durand-Riard, P., L. Salles, M. Ford, G. Caumon, and J. Pellerin, 2011, Understanding the evolution of syn-depositional folds: Coupling decompaction and 3D sequential restoration: Marine and Petroleum Geology, v. 28, no. 8, p. 1530–1539, doi:10.1016/j.marpetgeo.2011.04.001.
Eiken, O., P. Ringrose, C. Hermanrud, B. Nazarian, T. A. Torp, and L. Høier, 2011, Lessons learned from 14 years of CCS operations: Sleipner, In Salah and Snøhvit: Energy Procedia, v. 4, p. 5541–5548, doi:10.1016/j.egypro.2011.02.541.
Finlayson, D. M., C. D. N. Collins, I. Lukaszyk, and E. C. Chudyk, 1998, A transect across Australia’s southern margin in the Otway Basin region: Crustal architecture and the nature of rifting from wide-angle  seismic
seismic profiling: Tectonophysics, v. 288, no. 1, p. 177–189, doi:10.1016/S0040-1951(97)00291-6.
profiling: Tectonophysics, v. 288, no. 1, p. 177–189, doi:10.1016/S0040-1951(97)00291-6.
Freeman, B., D. J. Quinn, C. G. Dillon, M. Arnhild, and B. Jaarsma, 2015, Predicting subseismic fracture density and orientation in the Gorm Field, Danish North Sea, in F. L. Richards, N. J. Richardson, S. J. Rippington, R. W. Wilson, and C. E. Bond, eds., Industrial structural geology: Principles, techniques and integration: Geological Society, London, Special Publications 2015, v. 421, p. 231–244, doi:10.1144/SP421.9.
Geoscience Australia and Australian Stratigraphy Commission, 2017, Australian stratigraphic units database, accessed November 19, 2018, http://www.ga.gov.au/data-pubs/datastandards/stratigraphic-units.
Gibbs, A. D., 1983, Balanced cross-section construction from  seismic
seismic sections in areas of extensional tectonics: Journal of Structural Geology, v. 5, no. 2, p. 153–160, doi:10.1016/0191-8141(83)90040-8.
sections in areas of extensional tectonics: Journal of Structural Geology, v. 5, no. 2, p. 153–160, doi:10.1016/0191-8141(83)90040-8.
Groshong, J. R., and H. Richard, 1989, Half-graben structures: Balanced models of extensional fault-bend folds: Geological Society of America Bulletin, v. 101, no. 1, p. 1329–1360, doi:10.1130/0016-7606(1989)101<0096:HGSBMO>2.3.CO;2.
Guzofski, C. A., J. P. Mueller, J. H. Shaw, P. Muron, D. A. Medwedeff, F. Bilotti, and C. Rivero, 2009, Insights into the mechanisms of fault-related folding provided by volumetric structural restorations using spatially varying mechanical constraints: AAPG Bulletin, v. 93, no. 4, p. 479–502, doi:10.1306/11250807130.
Hauge, T. A., and G. G. Gray, 1996, A critique of techniques for  modeling
modeling normal-fault and rollover geometries, in P. G. Buchanan and D. A. Nieuwland, eds., Modern developments in structural interpretation, validation and
normal-fault and rollover geometries, in P. G. Buchanan and D. A. Nieuwland, eds., Modern developments in structural interpretation, validation and  modeling
modeling : Geological Society, London, Special Publications 1996, v. 99, p. 89–97, doi:10.1144/GSL.SP.1996.099.01.08.
: Geological Society, London, Special Publications 1996, v. 99, p. 89–97, doi:10.1144/GSL.SP.1996.099.01.08.
Hunt, L., S. Reynolds, T. Brown, S. Hadley, J. Downton, and S. Chopra, 2010, Quantitative estimate of fracture density variations in the Nordegg with azimuthal AVO and curvature: A case study: The Leading Edge, v. 29, no. 9, p. 1122–1137, doi:10.1190/1.3485773.
Isaacs, C. M., 1981, Porosity reduction during diagenesis of the Monterey Formation, Santa Barbara coastal area, in R. E. Garrison, R. G. Douglas, K. E. Pisciotto, C. M. Isaacs, and J. C. Ingle, eds., The Monterey Formation and related siliceous rocks of California: Los Angeles, SEPM Pacific Section, Special Publication 15, p. 257–272.
Jones, M. E., and M. A. Addis, 1984, Volume change during sediment diagenesis and the development of growth faults: Marine and Petroleum Geology, v. 1, no. 2, p. 118–122, doi:10.1016/0264-8172(84)90081-3.
Keating, E., D. Newell, D. Dempsey, and R. Pawar, 2014, Insights into interconnections between the shallow and deep systems from a natural CO2 reservoir near Springerville, Arizona: International Journal of Greenhouse Gas Control, v. 25, p. 162–172, doi:10.1016/j.ijggc.2014.03.009.
Krassay, A. A., D. L. Cathro, and D. J. Ryan, 2004, A regional tectonostratigraphic framework for the Otway Basin, in P. J. Boult, D. R. Johns, and S. C. Lang, eds., Eastern Australasian Basins Symposium II, Adelaide, South Australia, Australia, November 19–22, 2004, p. 97–116.
Krawczyk, C. M., and D. C. Tanner, 2010, Subseismic deformation analysis—A prediction tool for a safe CO2-reservoir management: Second European Association of Geoscientists and Engineers CO2 Geological Storage Workshop, Berlin, Germany, March 11–12, 2010, p. 1–5.
Krawczyk, C. M., D. C. Tanner, A. Henk, H. Trappe, and M. Urosevic, 2011, Sub-/ seismic
seismic deformation prediction—Development of a new seismo-mechanical workflow in the Otway Basin: Proceedings of the 1st Sustainable Earth Sciences Conference and Exhibition, Valencia, Spain, November 8–10, 2011, p. 1–5, doi:10.3997/2214-4609.20144172.
deformation prediction—Development of a new seismo-mechanical workflow in the Otway Basin: Proceedings of the 1st Sustainable Earth Sciences Conference and Exhibition, Valencia, Spain, November 8–10, 2011, p. 1–5, doi:10.3997/2214-4609.20144172.
Krawczyk, C. M., D. C. Tanner, A. Henk, J. Ziesch, T. Beilecke, C. M. Aruffo, and B. Weber, et al., 2015,  Seismic
Seismic and sub-
and sub- seismic
seismic deformation prediction in the context of geological carbon trapping and storage: Cham, Switzerland, Springer International Publishing AG, Advanced Technologies in Earth Sciences 22, p. 97–113, doi:10.1007/978–3–319–13930–2_5.
deformation prediction in the context of geological carbon trapping and storage: Cham, Switzerland, Springer International Publishing AG, Advanced Technologies in Earth Sciences 22, p. 97–113, doi:10.1007/978–3–319–13930–2_5.
La Pointe, P. R., J. Hermanson, R. Parney, T. Eiben, M. Dunleavy, K. Steele, J. Whitney, D. Eubanks, and R. Straub, 2002, 3-D reservoir and stochastic fracture network  modeling
modeling for enhanced oil recovery, Circle Ridge Phosphoria/Tensleep Reservoir, Wind River Reservation, Arapaho and Shoshone Tribes, Wyoming: Tulsa, Oklahoma, US Department of Energy Technical Report DE-FG-00BC15190, 221 p.
for enhanced oil recovery, Circle Ridge Phosphoria/Tensleep Reservoir, Wind River Reservation, Arapaho and Shoshone Tribes, Wyoming: Tulsa, Oklahoma, US Department of Energy Technical Report DE-FG-00BC15190, 221 p.
Lawver, L. A., L. M. Gahagan, and I. W. D. Dalziel, 2011, A different look at gateways: Drake Passage and Australia/Antarctica, in J. B. Anderson and J. S. Wellner, eds., Tectonic, climatic and cyrospheric evolution of the Antarctic Peninsula: Washington, DC, American Geophysical Union Special Publication 63, p. 5–34, doi:10.1029/2010SP001017.
Lisle, R. J., 1994, Detection of zones of abnormal strains in structures using gaussian curvature analysis: AAPG Bulletin, v. 78, no. 12, p. 1811–1819.
Lohr, T., C. M. Krawczyk, D. C. Tanner, R. Samiee, H. Endres, P. O. Thierer, O. Oncken, H. Trappe, R. Bachmann, and P. A. Kukla, 2008, Prediction of subseismic faults and fractures: Integration of three-dimensional  seismic
seismic data, three-dimensional retrodeformation, and well data on an example of deformation around an inverted fault: AAPG Bulletin, v. 92, no. 4, p. 473–485, doi:10.1306/11260707046.
data, three-dimensional retrodeformation, and well data on an example of deformation around an inverted fault: AAPG Bulletin, v. 92, no. 4, p. 473–485, doi:10.1306/11260707046.
Mansfield, C. S., and J. A. Cartwright, 2001, Fault growth by linkage: Observations and implications from analogue models: Journal of Structural Geology, v. 23, no. 5, p. 745–763, doi:10.1016/S0191–8141(00)00134–6.
Marrett, R., and R. W. Allmendinger, 1992, Amount of extension on “small” faults: An example from the Viking graben: Geology, v. 20, p. 47–50, doi:10.1130/0091–7613(1992)020.
Mathieson, A., J. Midgley, K. Dodds, I. Wright, P. Ringrose, and N. Saoul, 2010, CO2 sequestration monitoring and verification technologies applied at Krechba, Algeria: The Leading Edge, v. 29, p. 216–222, doi:10.1190/1.3304827.
Mohr, M., P. A. Kukla, J. L. Urai, and G. Bresser, 2005, Multiphase salt tectonic evolution in NW Germany:  Seismic
Seismic interpretation and retro-deformation: International Journal of Earth Sciences, v. 94, p. 917–940, doi:10.1007/s00531–005–0039–5.
interpretation and retro-deformation: International Journal of Earth Sciences, v. 94, p. 917–940, doi:10.1007/s00531–005–0039–5.
Moore, A. M. G., H. M. J. Stagg, and M. S. Norvick, 2000, Deep-water Otway Basin: A new assessment of the tectonics and hydrocarbon prospectivity: APPEA Journal, v. 40, p. 66–85, doi:10.1071/AJ99005.
Midland Valley Exploration Ltd., 2016, Move 2016.2 Software Suite, accessed March 4, 2019, https://www.mve.com.
Needham, T., G. Yielding, and R. Fox, 1996, Fault population description and prediction using examples from the offshore U.K.: Journal of Structural Geology, v. 18, no. 2–3, p. 155–167, doi:10.1016/S0191-8141(96)80041–1.
Nicol, A., J. Walsh, K. Berryman, and S. Nodder, 2005, Growth of a normal fault by the accumulation of slip over millions of years: Journal of Structural Geology, v. 27, no. 2, p. 327–342, doi:10.1016/j.jsg.2004.09.002.
Norden, B., 2011, Modelling of the near-surface groundwater flow system at the CO2SINK site Ketzin, Germany: Zeitschrift der Deutschen Gesellschaft für Geowissenschaften, v. 162, no. 1, p. 63–77, doi:10.1127/1860–1804/2011/0162–0063.
Norvick, M. S., and M. A. Smith, 2001, Mapping the plate tectonic reconstructions of southern and southeastern Australia and implications for petroleum system: APPEA Journal, v. 41, p. 15–35, doi:10.1071/AJ00001.
Perincek, D., and C. D. Cockshell, 1995, The Otway Basin: Early Cretaceous rifting to Neogene inversion: APPEA Journal, v. 35, p. 451–466, doi:10.1071/AJ94029.
Plesch, A., J. H. Shaw, and D. Kronman, 2007, Mechanics of low-relief detachment folding in the Bajiaochang Field, Sichuan Basin, China: AAPG Bulletin, v. 91, no. 11, p. 1559–1575, doi:10.1306/06200706072.
Ramsay, J. G., and M. I. Huber, 1983, The techniques of modern structural geology: Strain analysis, London, Academic Press, v. 1, 307 p.
Reston, R., and K. McDermott, 2014, An assessment of the cause of the ‘extension discrepancy’ with reference to the west Galicia margin: Basin Research, v. 26, no. 1, p. 135–153, doi:10.1111/bre.12042.
Riding, J. B., 2006, The IEA Weyburn CO2 monitoring and storage project, in S. Lombardi, L. K. Altunina, and S. E. Beaubien, eds., Advances in the geological storage of carbon dioxide: Dordrecht, the Netherlands, Springer, North Atlantic Treaty Organization Science Series: IV: Earth and Environmental Sciences 65, p. 221–230, doi:10.1007/1-4020-4471-2_18.
Ringrose, P. S., A. S. Mathieson, I. W. Wright, F. Selama, O. Hansen, R. Bissell, N. Saoula, and J. Midgley, 2013, The In Salah CO2 storage project: Lessons learned and knowledge transfer: Energy Procedia, v. 37, p. 6226–6236, doi:10.1016/j.egypro.2013.06.551.
Rouby, D., H. Xiao, and J. Suppe, 2000, 3-D restoration of complexy folded and faulted surfaces using multiple unfolding mechanisms: AAPG Bulletin, v. 84, no. 6, p. 805–829, doi:10.1306/A9673400-1738-11D7-8645000102C1865D.
Schultz-Ela, D. D., 1992, Restoration of cross-sections to constrain deformation processes of extensional terranes: Marine and Petroleum Geology, v. 9, no. 4, p. 372–388, doi:10.1016/0264–8172(92)90049–K.
Sclater, J. G., and P. A. F. Christie, 1980, Continental stretching: An explanation of the post mid-Cretaceous subsidence of the Central North Sea Basin: Journal of Geophysical Research, v. 85, p. 3711–3739, doi:10.1029/JB085iB07p03711.
Stork, A. L., J. P. Verdon, and J.-M. Kendall, 2014, The microseismic response at the In Salah Carbon Capture and Storage (CCS) site: International Journal of Greenhouse Gas Control, v. 32, p. 159–171, doi:10.1016/j.ijggc.2014.11.014.
Suo, C., S. Peng, S. Chang, R. Duan, and G. Wang, 2012, A new calculating method of the curvature to predicting the reservoir fractures: Procedia Environmental Sciences, v. 12, p. 576–582, doi:10.1016/j.proenv.2012.01.320.
Tupper, N. P., D. Padley, R. Lovibond, A. K. Duckett, and D. M. McKirdy, 1993, A key test of Otway Basin Potential: The Eumeralla-sourced play on the Charma Terrace: APPEA Journal, v. 33, no. 1, p. 77–93, doi:10.1071/AJ92007.
Trappe, H., and C. Hellmich, 2003,  Seismic
Seismic volume attributes for fracture analysis: Geological Society, London, Special Publications 2003, v. 209, p. 65–75, doi:10.1144/GSL.SP.2003.209.01.07.
volume attributes for fracture analysis: Geological Society, London, Special Publications 2003, v. 209, p. 65–75, doi:10.1144/GSL.SP.2003.209.01.07.
Tvedt, A. B. M., A. Rotevatn, A.-L. Jackson, H. Fossen, and R. L. Gawthorpe, 2013, Growth of normal faults in multilayer sequences: A 3D  seismic
seismic case study from the Egersund Basin, Norwegian North Sea: Journal of Structural Geology, v. 55, p. 1–20, doi:10.1016/j.jsg.2013.08.002.
case study from the Egersund Basin, Norwegian North Sea: Journal of Structural Geology, v. 55, p. 1–20, doi:10.1016/j.jsg.2013.08.002.
van der Pluijm, B., and S. Marshak, 2004, Earth structure: An introduction to structural geology and tectonics, 2nd ed.: New York, W. W. Norton and Company, 672 p.
Walsh, J. J., and J. Watterson, 1992, Populations of faults and fault displacements and their effects on estimates of fault-related regional extension: Journal of Structural Geology, v. 14, no. 6, p. 701–712, doi:10.1016/0191–8141(92)90127–I.
Watkins, H., R. W. H. Butler, C. E. Bond, and D. Healy, 2015, Influence of structural position on fracture networks in the Torridon Group, Achnashellach fold and thrust belt, NW Scotland: Journal of Structural Geology, v. 74, p. 64–80, doi:10.1016/j.jsg.2015.03.001.
Watkins, H., D. Healy, C. E. Bond, and R. W. H. Butler, 2018, Implications of heterogeneous fracture distribution on reservoir quality; an analogue from the Torridon Group sandstone, Moine Thrust Belt, NW Scotland: Journal of Structural Geology, v. 108, p. 180–197, doi:10.1016/j.jsg.2017.06.002.
Watson, M. N., C. J. Boreham, and P. R. Tingate, 2004, Carbon dioxide and carbonate cements in the Otway Basin: Implications for geological storage of carbon dioxide: APPEA Journal, v. 44, p. 703–720.
Watterson, J., J. J. Walsh, A. Gillespie, and S. Easton, 1996, Scaling systematics of fault sizes on a large-scale range fault map: Journal of Structural Geology, v. 18, no. 2–3, p. 199–214, doi:10.1016/S0191–8141(96)80045–9.
White, L. T., G. M. Gibson, and G. S. Lister, 2013, A reassessment of paleogeographic reconstructions of eastern Gondwana: Bringing geology back into the equation: Gondwana Research, v. 24, p. 984–998, doi:10.1016/j.gr.2013.06.009.
White, N. J., J. A. Jackson, and D. P. McKenzie, 1986, The relationship between the geometry of normal faults and that of sedimentary layers in their hanging walls: Journal of Structural Geology, v. 8, p. 897–909, doi:10.1016/0191–8141(86)90035–0.
Whittaker, S., B. Rostron, C. Hawkes, C. Gardner, D. White, J. Johnson, R. Chalaturnyk, and D. Seeburger, 2011, A decade of CO2 injection into depleting oil fields: Monitoring and research activities of the IEA GHG Weyburn-Midale CO2 Monitoring and Storage Project: Energy Procedia, v. 4, p. 6069–6076, doi:10.1016/j.egypro.2011.02.612.
Williams, G., and I. Vann, 1987, The geometry of listric normal faults and deformation in their hangingwalls: Journal of Structural Geology, v. 9, no. 7, p. 789–795, doi:10.1016/0191–8141(87)90080–0.
Williamson, P. E., M. G. Swift, G. W. O’Brien, and D. A. Falvey, 1990, Two-stage Early Cretaceous rifting of the Otway Basin margin of southeastern Australia: Implications for rifting of the Australian southern margin: Geology, v. 18, no. 1, p. 75–78, doi:10.1130/0091-7613(1990)018<0075:TSECRO>2.3.CO;2.
Withjack, M. O., and E. T. Peterson, 1993, Prediction of normal-fault geometries—A sensitivity analysis: AAPG Bulletin, v. 77, no. 11, p. 1860–1873.
Xiao, H., and J. Suppe, 1992, Origin of a rollover: AAPG Bulletin, v. 76, no. 4, p. 509–529.
Yamada, Y., and K. McClay, 2003, Application of geometric models to inverted listric fault systems in sandbox experiments. Paper 2: Insights for possible along strike migration of material during 3D hanging wall deformation: Journal of Structural Geology, v. 25, p. 1331–1336, doi:10.1016/S0191-8141(02)00160-8.
Ziesch, J., C. M. Aruffo, D. C. Tanner, T. Beilecke, T. Dance, A. Henk, B. Weber, E. Tenthorey, A. Lippmann, and C. M. Krawczyk, 2017, Geological structure of the CO2CRC Otway Project site, Australia: Fault kinematics based on quantitative 3D  seismic
seismic interpretation: Basin Research, v. 29, no. 2, p. 129–148, doi:10.1111/bre.12146.
interpretation: Basin Research, v. 29, no. 2, p. 129–148, doi:10.1111/bre.12146.
Ziesch, J., D. C. Tanner, T. Beilecke, and C. M. Krawczyk, 2015, Fault kinematics based on quantitative 3-D  seismic
seismic interpretation: Geotectonic Research, v. 97, p. 108–111, doi:10.1127/1864-5658/2015-41.
interpretation: Geotectonic Research, v. 97, p. 108–111, doi:10.1127/1864-5658/2015-41.
AUTHORS
Jennifer Ziesch received her B.Sc. degree in 2007, her diploma in geosciences in 2010 at University of Göttingen, Germany, and her Ph.D. at Technical University of Berlin in 2016. Her research focuses on  seismic
seismic interpretation, fault analysis, and structural restoration. She is now head of the Cartography and Three-Dimensional
interpretation, fault analysis, and structural restoration. She is now head of the Cartography and Three-Dimensional  Modeling
Modeling Department at the State Authority for Mining, Energy and Geology in Hannover, Germany.
Department at the State Authority for Mining, Energy and Geology in Hannover, Germany.
David Tanner earned a B.Sc. degree in geology from Liverpool University, United Kingdom; an M.Sc. degree from Imperial College, London, United Kingdom; and a doctorate from Giessen University, Germany. His interests lie in structural geology. He specializes in three-dimensional kinematic  modeling
modeling of complexly deformed terrains. He is presently coordinator for topical research on terrestrial sediment systems and researcher in the
of complexly deformed terrains. He is presently coordinator for topical research on terrestrial sediment systems and researcher in the  Seismic
Seismic Gravimetry, and Magnetics section at the Leibniz Institute for Applied Geophysics.
Gravimetry, and Magnetics section at the Leibniz Institute for Applied Geophysics.
Charlotte Krawczyk is the director of the Geophysics Department at GFZ Potsdam and is a professor of geophysics at Technical University of Berlin. Her scientific interests comprise  seismic
seismic methods and technical developments in applied geophysics, subseismic deformation analysis, and geophysical imaging of deformation and mass transport. She currently serves as the executive editor of Solid Earth, and she is a member of Acatech and AcademiaNet.
methods and technical developments in applied geophysics, subseismic deformation analysis, and geophysical imaging of deformation and mass transport. She currently serves as the executive editor of Solid Earth, and she is a member of Acatech and AcademiaNet.
ACKNOWLEDGMENTS
This work was sponsored in part by the Australian Commonwealth Government through the Cooperative Research Centre for Greenhouse Gas Technologies. Prediction of Deformation to Ensure Carbon Traps is funded through the Geotechnologien research program in Germany (03G0797, publication no. GEOTECH-2215). We thank Midland Valley Exploration Limited for an academic license for the software Move. We thank T. Beilecke, R. Groshong Jr., J. Stewart, G. Yielding, C. A. Guzofski, B. Willis, and AAPG Editor Barry J. Katz for constructive discussion and their reviews.
